AI摘要:本文详细讨论了超声在球面声场中的传播特性。首先,通过声波波动方程和赫姆霍兹方程,推导出了声波的通用解。接着,通过分析球面声波的产生和传播过程,得到了球面声波方程的解。文章还探讨了球面声场中声压和声速的计算方法,并分析了声源半径与声波波长的关系。最后,讨论了点声源在自由空间和半空间情况下的声压特性。
Powered by AISummary.
超声——球面声场
声波方程的通用解
根据声波波动方程:$\frac{\partial^2 p}{\partial x^2}=\frac{1}{C_s^2}\frac{\partial^2 p}{\partial^2t}$,这是一个二阶线性偏微分方程,采用分离变量法求解。使用复数表示为:
$p(x,t)=p(x)e^{jwt}$
代入后为:
$e^{jwt}\frac{\partial^2 p(x,t)}{\partial x^2}=\frac{1}{C_s^2}p(x)(jw)(jw)e^{jwt}$
$\frac{\partial^2 p(x,t)}{\partial x^2}=-\frac{w^2}{C_s^2}p(x,t)$,这其中$k=\frac{w}{C_s}=\frac{2\pi f}{C_s}=\frac{2\pi}{\lambda}$为波数。
$\frac{\partial^2 p(x,t)}{\partial x^2}+\frac{w^2}{C_s^2}p(x,t)=0$,这个是赫姆霍兹方程(Helmholtz function),这里面与t无关,其通解为三角函数的组合:
$p(x)=Ae^{-jkx}+Be^{jkx}$
则$p(x,t)=p(x)e^{jwt}=(Ae^{-jkx}+Be^{jkx})e^{jwt}=Ae^{j(wt-kx)}+Be^{j(wt+kx)}$。
假设$f(t)=Ae^{jwt}$,则$f(t-x')=Ae^{j(w(t-x'))}=Ae^{jwt-jwx'}=Ae^{j(wt-kx)}$,得$x=\frac{wx'}{k}=C_sx'$。
对于$f(t-x’)$,其表示t往前移动x'。因为原来f(t=0)=A,现在需要f(t=x')=A,这说简单的说明了t需要移动到x‘,不考虑x'的正负号就是往前移动了x'。
所以$Ae^{j(wt-kx)}$表示沿着x正向传播,而$Be^{j(wt+kx)}$则表示反向传播。
假定介质是无限大的,没有反射波,则B=0。故最终为:
$p(x,t)=Ae^{j(wt-kx)}$
当x=0时,$p(0,t)=Ae^{jwt}$,定义$A=p_a$,则为:$p(x,t)=p_ae^{j(wt-kx)}$
球面声波方程
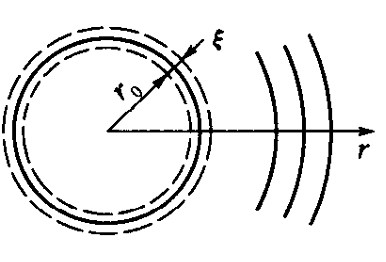
假设有这样一个声源,半径为r0的球体,表面做均匀的膨胀收缩,膨胀收缩位移为ξ(或者dr),面积为S(随着位移变化),该振动产生了声波。球面的振动过程具有各向均匀的脉动性质,因此产生的声波波阵面是球面,辐射的是均匀球面波。
根据声波推导过程,其三个方程为如下。
运动方程:$\rho_0 \frac{\partial v }{\partial t}=-\frac{\partial p}{\partial r} $
连续性方程:单位时间内流入与流出微元的质量差等于微元内密度变化引起的质量的增量,这里面积是个变量,与半径的变化有关,故不能消掉。
$\frac{\partial \rho}{\partial t}Sdr=(\rho v)_r S-(\rho v)_{r+dr}S=-\frac{\partial{\rho v S}}{\partial r}dr$,其中ρ仍是个变量为$\rho_0+\rho^{'}=\rho_0+d\rho$,密度是在单位时间内变化的与r无关,代入后为:
$\frac{\partial \rho'}{\partial t}S=-\rho_0\frac{\partial{v S}}{\partial r}=-\rho_0(v\frac{\partial S}{\partial r}+S\frac{\partial v}{\partial r})$
根据物态方程:$p=C_o^2\rho '$,得$\frac{\partial p}{\partial t}=C_o^2\frac{\partial \rho'}{\partial t}$,联立两者为:$\frac{\partial p}{\partial t}\frac{S}{C_0^2}=-\rho_0(v\frac{\partial S}{\partial r}+S\frac{\partial v}{\partial r})$,则可得:
$\frac{\partial p}{\partial t}=-\rho_0 C_0^2(v\frac{1}{S}\frac{\partial S}{\partial r}+\frac{\partial v}{\partial r})=-\rho_0 C_0^2(v\frac{\partial lnS}{\partial r}+\frac{\partial v}{\partial r})$
运动方程对r求偏导为:$\rho_0 \frac{\partial v }{\partial t}\frac{\partial v }{\partial r}=-\frac{\partial^2 p}{\partial r^2}$
物态方程对t求偏导为:$\frac{\partial^2 p}{\partial t^2}=-\rho_0 C_0^2(\frac {\partial (v\frac{\partial lnS}{\partial r})}{\partial t}+\frac{\partial v}{\partial r}\frac{\partial v}{\partial t})$
其中前者为$\frac {\partial (v\frac{\partial lnS}{\partial r})}{\partial t}=\frac {\partial v}{\partial t}\frac {\partial lnS}{\partial r}+v(\frac{\partial (\frac{\partial lnS}{\partial r}))}{\partial t}$,后项为二阶偏微分忽略不计,则变为:$\frac {\partial v}{\partial t}\frac {\partial lnS}{\partial r}$
其中后者为$\frac{\partial v}{\partial r}\frac{\partial v}{\partial t}=-\frac{\partial^2 p}{\partial r^2}\frac{1}{\rho_0}$
$\frac{\partial^2 p}{\partial t^2}=-\rho_0 C_0^2 (\frac {\partial v}{\partial t}\frac {\partial lnS}{\partial r}-\frac{\partial^2 p}{\partial r^2}\frac{1}{\rho_0})=C_0^2(-\rho_0 \frac {\partial v}{\partial t}\frac {\partial lnS}{\partial r})+C_0^2 \frac{\partial^2 p}{\partial r^2}=C_0^2 \frac {\partial p}{\partial r}\frac {\partial lnS}{\partial r}+C_0^2 \frac{\partial^2 p}{\partial r^2}$
C0移到左边变为:
$\frac{1}{C_0^2}\frac{\partial^2 p}{\partial t^2}= \frac {\partial p}{\partial r}\frac {\partial lnS}{\partial r}+ \frac{\partial^2 p}{\partial r^2}$
因为球的面积为:$S=4\pi r^2$,则$\frac {\partial lnS}{\partial r}=\frac {\partial lnS}{\partial S}\frac {\partial S}{\partial r}=\frac{1}{4\pi r^2}4\pi 2r=\frac{2}{r}$,故上式为:$\frac{1}{C_0^2}\frac{\partial^2 p}{\partial t^2}=\frac {\partial p}{\partial r}\frac {2}{ r}+ \frac{\partial^2 p}{\partial r^2}$
假设Y=pr,则:$\frac{\partial Y}{\partial r}=p+r\frac{\partial p}{\partial r}$,$\frac{\partial^2 Y}{\partial r^2}=\frac{\partial p}{\partial r}+\frac{\partial p}{\partial r}+r\frac{\partial^2 p}{\partial^2 r}=2\frac{\partial p}{\partial r}+r\frac{\partial^2 p}{\partial^2 r}=r(\frac{2}{r}\frac{\partial p}{\partial r}+\frac{\partial^2 p}{\partial^2 r})=\frac{r}{C_0^2}\frac{\partial^2 p}{\partial t^2}$
又$\frac{\partial Y}{\partial t}=r\frac{\partial p}{\partial t}+p\frac{\partial r}{\partial t}=r\frac{\partial p}{\partial t}$,r和t都是独立变量,故偏微分为0。所以$\frac{\partial^2 Y}{\partial t^2}=r\frac{\partial^2 p}{\partial t^2}$
综合上式为:$\frac{\partial^2 Y}{\partial r^2}=\frac{1}{C_0^2}\frac{\partial^2 Y}{\partial t^2}$
即得最终式子为:
$\frac{\partial^2 (pr)}{\partial r^2}=\frac{1}{C_0^2}\frac{\partial^2 (pr)}{\partial t^2}$
根据声波方程求解,可知:$Y=pr=Ae^{j(wt-kr)}$,得到:$p=\frac{A}{r}e^{j(wt-kr)}$
球面声场
假设球面振动速度为:$v=v_re^{jwt}$,球面压力为:$p=p_re^{jwt}$,则:$p_r=\frac{A}{r}e^{-jkr}$
根据运动方程:$\rho_0 \frac{\partial v }{\partial t}=-\frac{\partial p}{\partial r} $。
首先计算v的偏微分:$\frac{\partial v }{\partial t}=v_rjwe^{jwt}=jwv_re^{jwt}$
齐次计算p的偏微分:$\frac{\partial p}{\partial r}=e^{jwt}\frac{\partial p_r}{\partial r}$
联立两式为:$\rho_0jwv_re^{jwt}=-e^{jwt}\frac{\partial p_r}{\partial r}$,可得:
$v_r=-\frac{1}{j\rho_0w}\frac{\partial p_r}{\partial r}=-\frac{1}{j\rho_0w}(-e^{-jkr}\frac{A}{r^2}+\frac{A}{r}(-jk)e^{-jkr})=-e^{-jkr}\frac{1}{j\rho_0w}(-\frac{A}{r^2}-\frac{jkA}{r})=Ae^{-jkr}\frac{1}{j\rho_0w}(\frac{1}{r^2}+\frac{jk}{r})$
故得到v为:
$v=v_re^{jwt}=Ae^{j(wt-kr)}\frac{1}{j\rho_0w}(\frac{1}{r^2}+\frac{jk}{r})=\frac{A}{\rho_0kC_0}(\frac{1}{jr^2}+\frac{k}{r})e^{j(wt-kr)}=\frac{A}{\rho_0C_0r}(1+\frac{1}{jkr})e^{j(wt-kr)}$
球源表面处的介质质点速度等于球源表面的振动速度,假设球源表面的振动速度为(球源在半径a处):$u=u_ae^{j(wt-ka)}$
对比上式在半径r处的声速,可得:$u_a=\frac{A}{\rho_0C_0a}(1+\frac{1}{jka})=\frac{A}{\rho_0C_0ajka}(1+jka)=\frac{A}{j\rho_0C_0ka^2}(1+jka)$
则可计算出A为:$A=\frac{j\rho_0C_0ka^2}{1+jka}u_a=\frac{\rho_0C_0ka^2}{(-1+jka)(1+jka)}u_a(1+jka)=\frac{\rho_0C_0ka^2}{(1+(ka)^2)}u_a(1+jka)$
A的模为:$|A|=\frac{\rho_0C_0ka^2}{\sqrt{1+(ka)^2}}u_a$,角度为:$\theta=arctan(\frac{1}{ka})$
声压为:$p=\frac{|A|}{r}e^{j(wt-kr+\theta)}$
声速v为:$v=\frac{A}{\rho_0C_0r}(1+\frac{1}{jkr})e^{j(wt-kr)}=\frac{|A|}{\rho_0C_0r}(1+\frac{1}{jkr})e^{j(wt-kr+\theta)}=|A|e^{j(wt-kr+\theta)}(\frac{1-j\frac{1}{kr}}{\rho_0C_0r})$
后者假设为B:$B=\frac{1-j\frac{1}{kr}}{\rho_0C_0r}$,其模为:$|B|=\frac{\sqrt{1+(\frac{1}{kr})^2}}{\rho_0C_0r}=\frac{1}{r}\frac{\sqrt{1+(kr)^2}}{\rho_0C_0kr}$,角度为:$\theta'=arctan(-\frac{1}{kr})$
则最终的v为:$v=|A||B|e^{j(wt-kr+\theta+\theta')}$
假设Q为声源强度(体积速度)为:$Q=u_a S=4\pi a^2u_a$,可以得到声压为:
$|p|=\frac{|A|}{r}=\frac{\rho_0C_0ka^2}{r\sqrt{1+(ka)^2}}u_a=\frac{\rho_0C_0ka^2}{r\sqrt{1+(ka)^2}}\frac{Q}{4\pi a^2}=\frac{\rho_0C_0kQ}{4\pi r\sqrt{1+(ka)^2}}$
则可得v的模,即:$|v|=|A||B|=\frac{\rho_0C_0ka^2}{\sqrt{1+(ka)^2}}\frac{1}{r}\frac{\sqrt{1+(kr)^2}}{\rho_0C_0kr}=\frac{Q}{4\pi r^2}\frac{\sqrt{1+(kr)^2}}{\sqrt{1+(ka)^2}}$
当a<<λ时,即声源半径远小于声波波长时,$ka=2\pi\frac{a}{\lambda}<<1$
则$|A|=\rho_0C_0ka^2u_a$,$\theta=\frac{\pi}{2}$,$p=j\frac{\rho_0C_0kQ}{4\pi r}e^{j(wt-kr)}$,$v=j\frac{Q\sqrt{1+(kr)^2}}{4\pi r^2}e^{j(wt-kr+\theta')}$
当a>>λ时,即声源半径远大于声波波长时,$ka=2\pi\frac{a}{\lambda}>>1$
则$|A|=\frac{\rho_0C_0ka^2}{\sqrt{1+(ka)^2}}u_a=\frac{\rho_0C_0ka^2}{ka}u_a=\rho_0C_0au_a$,$\theta=0$,$p=\frac{\rho_0C_0 Q}{4 \pi a r}e^{j(wt-kr)}$
点声源
对于自由空间点声源,其相当于球源,但是点声源的半径r<<λ,故声压为:
$p=j\frac{\rho_0C_0kQ}{4\pi r}e^{j(wt-kr)}$
若是半空间的点声源,即另外一半是硬边界,仅有半个球源,则其声源强度为:$Q=u_a S/2=2\pi a^2u_a$,其声压为:
$p=j\frac{\rho_0C_0kQ}{2\pi r}e^{j(wt-kr)}$

