AI摘要:本文介绍了如何通过动力学方程、连续性方程和物态方程推导出声波的波动方程。首先,动力学方程描述了流体体积元在声压作用下的运动,连续性方程描述了流体质量守恒,物态方程则描述了声波过程中的绝热关系。通过这些方程的推导和联立,我们可以得到声波的一维波动方程,即声压和密度的变化遵循波动方程。
Powered by AISummary.
超声——声波波动方程推导
根据3个物理学方程可以推导出声波的波动方程:
- 动力学方程
- 连续性方程
- 物态方程
假设前提:
- 介质为理想流体,无粘滞和热传导导致热损耗
- 无声波时介质静止不动,宏观上均匀。静压P0,静密度ρ0
- 声波传播过程是绝热,无热交换
- 介质中声波是小振幅声波
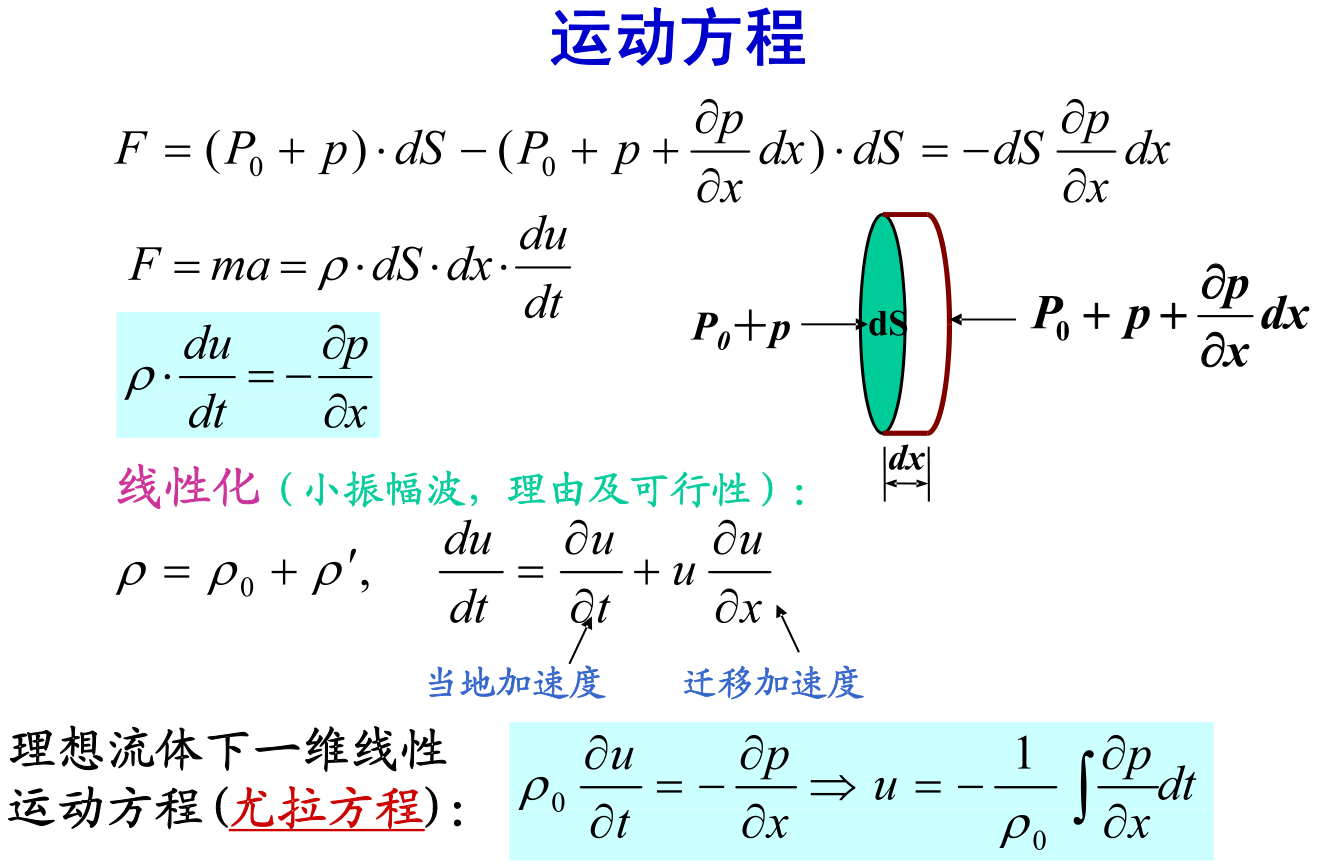
动力学方程
其又称运动方程,或者牛顿第二定律。
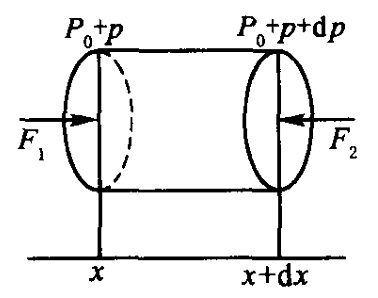
假设模型如上图所示。
一个流体体积元截面积为S,因为声压p导致流体流动,流到距离为dx,则流动体积为$Sdx$。流体从x到x+dx,声压是不同的,故p与x有关,即$p∝x$。
x处压力与x+dx压力不相等,这导致了流体的运动。前后所受的力是压强与面积的积。
$F_1=(P_0 + p)S$
$F_2=(P_0 + p + dp)S$
该流体的质量为$ρSdx$ ,根据牛顿第二定律:$F=ma^2$。加速度为:$a = \frac{dv}{dt}$,则有
$ρSdx\frac{dv}{dt}=F_1 - F_2=-Sdp$
$ρdx\frac{dv}{dt}=-dp$
增加的dp为p对x的偏微分:$dp=\frac{\partial{p}}{\partial{x}}dx $
联合后为:
$ρdx\frac{dv}{dt}=-dp=-\frac{\partial{p}}{\partial{x}}dx $
化简后为:
$ρ\frac{dv}{dt}=-\frac{\partial{p}}{\partial{x}}$
这里其实已经推导出来,但是严格的说,ρ仍是个变量为$\rho_0+\rho^{'}=\rho_0+d\rho$,$\rho^{'}$相当于密度增量$d\rho$,而且速度是与x和t同时相关的变量。则上式子为:
$(\rho_0 +\rho ^{'} )(\frac{\partial v }{\partial t }+v\frac{\partial v }{\partial x } )=-\frac{\partial p}{\partial x} $
由于是小振幅声波,故二次量可以忽略。最终为:
$\rho_0 \frac{\partial v }{\partial t}=-\frac{\partial p}{\partial x} $
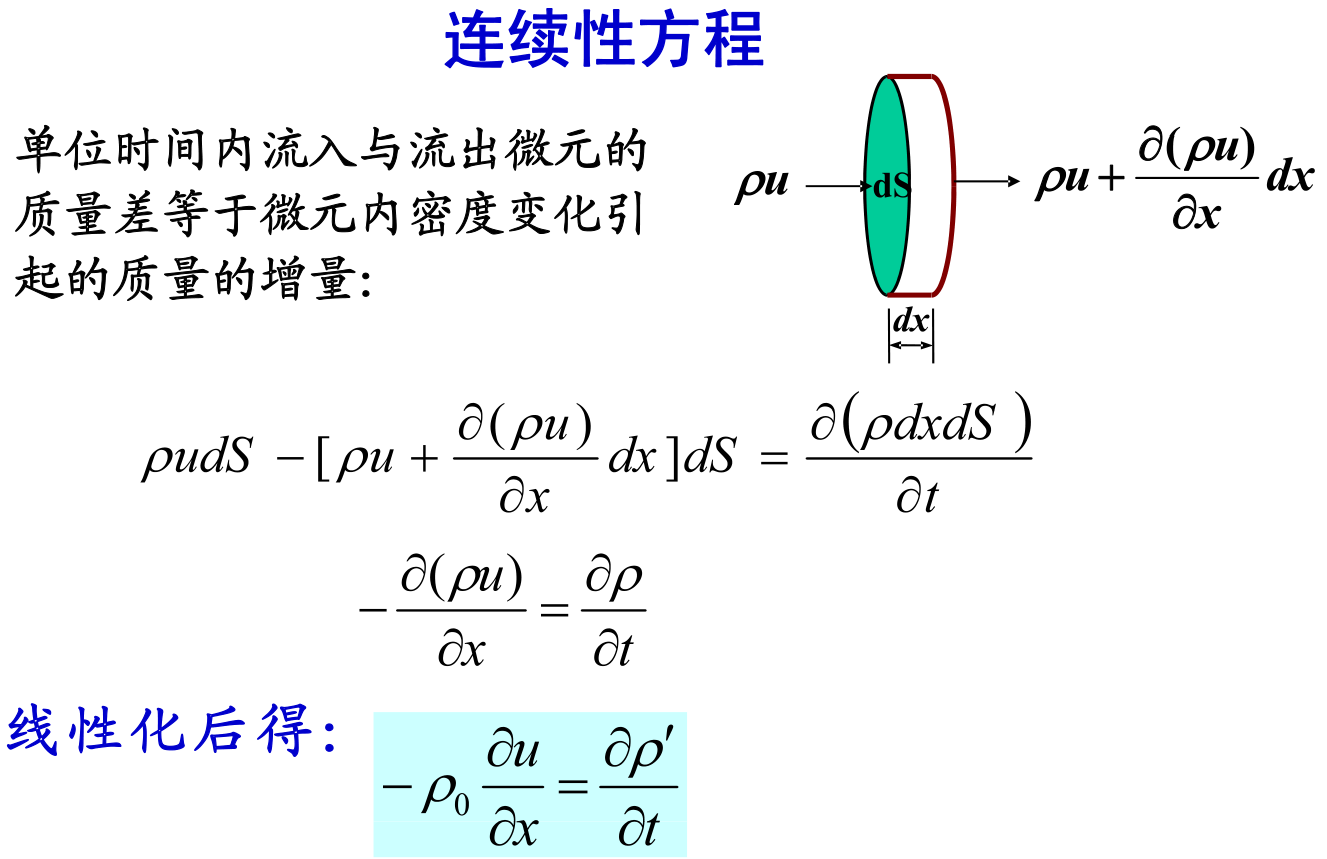
连续性方程
其又称质量守恒定理,即单位时间内流体流入和流出的质量差等于流体内的质量变化。
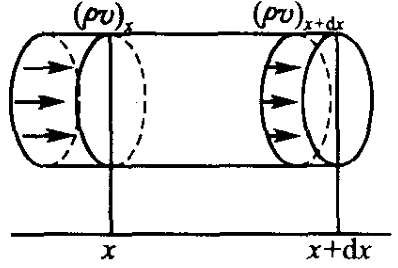
流入的流体体积为高度乘以面积(圆柱体):$(\rho v)_x$
流出的则为:$(\rho v)_{x+dx}$
质量为密度乘以体积,故流入和流出的质量差为:$(\rho v)_x S-(\rho v)_{x+dx}S$
因为质量的流入和流出导致了密度的变化,密度是在单位时间内变化的,故根据密度和距离x的变化可以计算出质量的变化:
$\frac{d\rho}{dt}Sdx=(\rho v)_x S-(\rho v)_{x+dx}S$
$\frac{d\rho}{dt}dx=(\rho v)_x -(\rho v)_{x+dx}$
根据泰勒展开$(\rho v)_{x+dx}=(\rho v)_x+ \frac{\partial \rho v }{\partial x}dx$
得到$-\frac{\partial \rho v }{\partial x}dx=\frac{d\rho}{dt}dx$
最终为:
$-\frac{\partial \rho v }{\partial x}=\frac{d\rho}{dt}$
同样,严格的说ρ仍是个变量为$\rho_0+\rho^{'}=\rho_0+d\rho$,$\rho^{'}$相当于密度增量$d\rho$,代入后为:
$\frac{\partial (\rho_0 + \rho^{'}) v }{\partial x}=-\frac{\partial (\rho_0 + \rho^{'})}{\partial t} $
$\frac{\partial (\rho_0 + \rho^{'}) v }{\partial x}=v\frac{\partial (\rho_0+\rho^{'} ) }{\partial x } +(\rho_0+\rho^{'})\frac{\partial v }{\partial x } $
$v\frac{\partial \rho_0 }{\partial x } +v\frac{\partial\rho^{'}}{\partial x } +\rho_0\frac{\partial v }{\partial x } +\rho^{'}\frac{\partial v }{\partial x }$
$\rho_0$为常数,偏微分为0。忽略掉二阶项。则为:
$\rho_0\frac{\partial v }{\partial x }=-\frac{\partial \rho^{'}}{\partial t}$
物态方程
又称为热力学第一定律。同时考虑到声波过程进程比较快,体积压缩和膨胀过程的时间要比热传导需要的时间短很多,故认为声波过程中时绝热过程。
绝热过程中Q=0,即外界传递给系统的能量为0。
根据热力学第一定律:
$A = U_2 - U_1=\int_{T_1}^{T_2}C_vdT $
A:外界对系统做的功
U2:初态内能
U1:末态内能
Cv:定体热容(指在体积保持不变的条件下,系统吸收或放出的热量与温度变化量的比值)
T:温度
根据玻意耳定律(Boyle's law):在定量定温下,理想气体的体积与气体的压强成反比。
其数学表达式为$pV=C_1$(p为压强,V为体积,C1为常数)。
根据查理定律:一定质量的气体,在体积保持不变时,压强与热力学温度成正比。
其数学表达式为$p=C_2T$(C2为常数,与气体的物质的量、体积有关)。
根据盖-吕萨克定律:一定质量的气体,在压强保持不变时,其体积与热力学温度成正比。
其数学表达式为$V=C_3T$(C3为常数,与气体的物质的量、压强有关)。
结合3个定律可得:$\frac{pV}{T}=C$,C为常数。
根据阿伏伽德罗定律(Avogadro's law):在相同的温度和压强下,相同体积的任何气体都含有相同数目的分子,即气体的物质的量与体积成正比。
在T0=273.15K、p0=1atm状态下,1mol的任何其他所占的体积为摩尔体积,1mol体积为w0=22.41410L/mol。假设气体的摩尔质量为M,气体的质量为m,则摩尔数为:$\vartheta =\frac{m}{M}=6.02 \times 10^{23} mol$。其体积为:$V_0 = \vartheta w_0 $。在T0时的方程如下:
$\frac{pV}{T}=\frac{p_0 \vartheta w_0}{T_0}=\vartheta R$
故理想气体的物态方程为:$pV=\vartheta R T$,其中R=8.31451 J/(mol*K)。
对物态方程进行对温度T的微分:$p\frac{dV}{dT}+V\frac{dp}{dT}=\vartheta R$
考虑如下的封闭活塞运动,压力f对气体做功,将活塞移动$\Delta l$的距离。
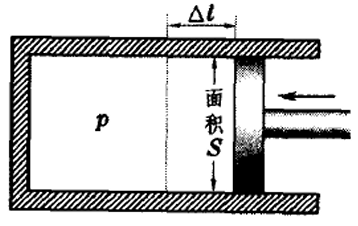
则所做的功为:$\Delta A=f\Delta l=-pS\Delta l=-p\Delta V$,压强是反向于f,故压力是反向于f。
对齐求积分可得:$A=-\int pdV$
当然,根据准静态过程的热力学第一定律:$\Delta U=U_2-U_1=Q-\int_{1}^{2} pdV$,由于绝热过程的Q=0,也能得到上式。
则可以得到两个式子:
$\frac{dA}{dV}=-p$
$\frac{dA}{dT}=C_v$
联立可得:$-\frac{p}{C_v}=\frac{dT}{dV}$
代入物态方程为:
$-p\frac{C_v}{p}+V\frac{dp}{-\frac{p}{C_v}dV}=\vartheta R$
$\frac{\vartheta R+C_v}{C_v}=-\frac{V}{p}\frac{dV}{dp}$
其中:$C_p=\vartheta R+C_v$,表示定压热容。可改写为:
$\gamma =\frac{C_p}{C_v}=-\frac{V}{p}\frac{dV}{dp}$
$\frac{dp}{p}=-\gamma \frac{dV}{V}$
上式对T求积分可得:$lnp+\gamma lnV=C$,即$pV^{\gamma}=C$,该式子称为泊松公式。
$\rho_0 \frac{\partial v }{\partial t}=-\frac{\partial p}{\partial x} $对x求偏微分为:$\rho _0 \frac{\partial^2 y}{\partial t\partial x}=- \frac{\partial^2 p}{\partial^2x} $
$\rho_0\frac{\partial v }{\partial x }=-\frac{\partial \rho^{'}}{\partial t}$对t求偏微分为:$\rho _0 \frac{\partial^2 y}{\partial x\partial t}=- \frac{\partial^2 \rho^{'}}{\partial^2t} $
则上式两边相等,得到:$\frac{\partial^2 p}{\partial^2x} =\frac{\partial^2 \rho^{'}}{\partial^2t} $
由于声波是绝热的,可以认为压强仅与密度相关,即压强与ρ有关,则有$\frac{\partial p}{\partial x}= \frac{\partial p}{\partial \rho} \frac{\partial \rho}{\partial x}=C_s^2\frac{\partial \rho}{\partial x}$。其中Cs为常数,为声速。
同时有$\frac{\partial^2 p}{\partial x^2}= \frac{\partial p}{\partial \rho} \frac{\partial^2 \rho}{\partial x^2}+\frac{\partial \rho}{\partial x}\frac{\partial (\frac{\partial p}{\partial \rho})}{\partial x}=\frac{\partial p}{\partial \rho} \frac{\partial^2 \rho}{\partial x^2}=\frac{\partial^2 \rho^{'}}{\partial^2t}=C_s\frac{\partial^2 \rho}{\partial x^2}$,该式子为一维波动方程。
将$\frac{\partial \rho}{\partial x}=\frac{1}{C_s^2}\frac{\partial p}{\partial x}$代入,则可得到:$\frac{\partial^2 p}{\partial x^2}=\frac{1}{C_s^2}\frac{\partial^2 p}{\partial^2t}$,该式子也为一维波动方程。




