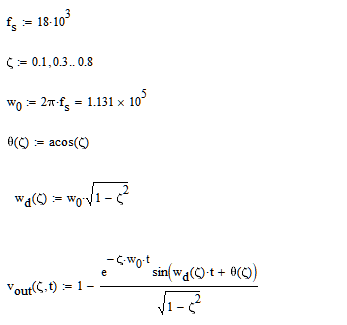AI摘要：本文介绍了二阶系统响应的基本概念和数学推导过程。首先，给出了二阶系统的传递函数和特征参数，包括自然频率、阻尼比和品质因数。然后，根据阻尼比的不同，讨论了过阻尼、临界阻尼和欠阻尼三种情况下的系统响应。接着，通过拉普拉斯变换、部分分式分解和三角恒等式，详细推导了欠阻尼情况下的RLC网络阶跃响应的时域表达式。最后，使用mathcad软件进行了计算验证。

Powered by AISummary.

二阶系统响应

《开关电源控制环路设计》之P3.3.1 二阶系统响应

概述

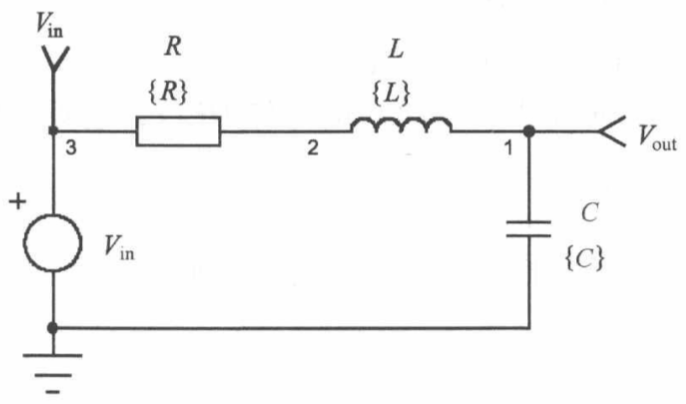
以上电路的传递函数为：

$V_{\text{out}}(s) = V_{\text{in}}(s) \frac{\frac{1}{sC}}{R + sL + \frac{1}{sC}}$

整理后为：

$\frac{V_{\text{out}}(s)}{V_{\text{in}}(s)} = \frac{1}{LCs^2 + RCs + 1}$

采用二阶系统表示：

$\frac{V_{\text{out}}(s)}{V_{\text{in}}(s)} = \frac{1}{\frac{s^2}{\omega_0^2} + 2\zeta \frac{s}{\omega_0} + 1} = \frac{1}{\frac{s^2}{\omega_0^2} + \frac{s}{\omega_0 Q} + 1}$

其中各式子表示为：

$\begin{gather*} \omega_0 = \frac{1}{\sqrt{LC}} \\ f_0 = \frac{\omega_0}{2\pi} = \frac{1}{2\pi \sqrt{LC}} \\ \zeta = \frac{1}{2Q} = \frac{R}{2} \sqrt{\frac{C}{L}} = \frac{RC\omega_0}{2} = \frac{R}{2L\omega_0} \\ Q = \frac{1}{2\zeta} = \frac{1}{R} \sqrt{\frac{L}{C}} = \frac{1}{RC\omega_0} = \frac{L\omega_0}{R} \end{gather*}$

其根为:

$\begin{gather*} s_1, s_2 = \frac{\omega_0}{2Q} \left( \pm \sqrt{1 - 4Q^2} - 1 \right) \\ s_1, s_2 = \omega_0 \zeta \left( \pm \sqrt{1 - \frac{1}{\zeta^2}} - 1 \right) \end{gather*}$

• 过阻尼：(Q<0.5)，根为不重合负实数，响应无振铃，如两级 RC 滤波器级联电路
• 临界阻尼：(Q = 0.5)，根为重合负实数，响应非振荡。根为：$s_{1,2} = -\omega_0$
• 欠阻尼：(Q>0.5)，根含虚数部分，响应振荡且因实部衰减，极点是负实部共轭复数，根为：

$s_{1,2} = -\frac{\omega_0}{2Q} \pm \mathrm{j}\omega_0 \sqrt{1 - \frac{1}{4Q^2}}$

$s_{1,2} = -\zeta\omega_0 \pm \mathrm{j}\omega_0 \sqrt{1 - \zeta^2}$

系统的阶跃响应为：

$v_{\text{out}}(t) = \mathcal{L}^{-1} \left( \frac{1}{s} \cdot \frac{1}{\frac{s^2}{\omega_0^2} + 2\zeta \frac{s}{\omega_0} + 1} \right)$

当$\zeta<1$时为欠阻尼状态，可推导上式中的阶跃响应。

推导过程(豆包生成)

要推导 RLC 网络阶跃响应（ζ<1 时）的时域表达式，需结合 拉普拉斯变换、部分分式分解、三角恒等式 逐步分析，以下是核心推导步骤：

步骤 1：确定系统传递函数与输入的拉普拉斯形式

设 RLC 网络的传递函数为 二阶系统标准形式，输入为阶跃信号（拉普拉斯变换为$frac{1}{s}
$ ），则系统输出的拉普拉斯域表达式为：

$V_{\text{out}}(s) = \frac{1}{s} \cdot \frac{1}{\frac{s^2}{\omega_0^2} + 2\zeta \frac{s}{\omega_0} + 1}$

将分母通分（乘以$ \omega_0^2$），整理为 二阶特征方程形式：

$V_{\text{out}}(s) = \frac{\omega_0^2}{s \left( s^2 + 2\zeta\omega_0 s + \omega_0^2 \right)}$

步骤 2：部分分式分解（ζ<1 时，分母有共轭复根）

当$$\zeta < 1$$ 时，分母的二次项$$s^2 + 2\zeta\omega_0 s + \omega_0^2$$ 有 共轭复根：

$s = -\zeta\omega_0 \pm j\omega_0\sqrt{1-\zeta^2} = -\sigma \pm j\omega_d$

其中，阻尼因子$ \sigma = \zeta\omega_0$，阻尼振荡角频率$ \omega_d = \omega_0\sqrt{1-\zeta^2}$。

对$V_{\text{out}}(s)$ 做 部分分式分解，设：

$V_{\text{out}}(s) = \frac{A}{s} + \frac{Bs + C}{s^2 + 2\zeta\omega_0 s + \omega_0^2}$

• 求常数项$A$：令$s=0$，两边乘$s$，得$A = \frac{\omega_0^2}{\omega_0^2} = 1$。
• 求分子$B, C$：通分后比较分子系数，得$B = -1$，$C = -2\zeta\omega_0$（推导见附录）。

因此：

$V_{\text{out}}(s) = \frac{1}{s} - \frac{s + 2\zeta\omega_0}{s^2 + 2\zeta\omega_0 s + \omega_0^2}$

步骤 3：配方与拉普拉斯逆变换

对二次项 配方（转化为复指数形式）：

$s^2 + 2\zeta\omega_0 s + \omega_0^2 = (s + \zeta\omega_0)^2 + \omega_0^2(1-\zeta^2) = (s + \sigma)^2 + \omega_d^2$

将分子$s + 2\zeta\omega_0$ 分解为$(s + \sigma) + \sigma$（因$2\zeta\omega_0 = \sigma + \sigma$），则：

$\frac{s + 2\zeta\omega_0}{(s + \sigma)^2 + \omega_d^2} = \frac{(s + \sigma) + \sigma}{(s + \sigma)^2 + \omega_d^2} = \frac{s + \sigma}{(s + \sigma)^2 + \omega_d^2} + \frac{\sigma}{\omega_d} \cdot \frac{\omega_d}{(s + \sigma)^2 + \omega_d^2}$

利用 拉普拉斯逆变换公式：

• $\mathcal{L}^{-1}\left\{ \frac{s + a}{(s + a)^2 + b^2} \right\} = e^{-at}\cos(bt)$
• $\mathcal{L}^{-1}\left\{ \frac{b}{(s + a)^2 + b^2} \right\} = e^{-at}\sin(bt)$

得逆变换：

$\mathcal{L}^{-1}\left\{ \frac{s + 2\zeta\omega_0}{(s + \sigma)^2 + \omega_d^2} \right\} = e^{-\sigma t}\cos(\omega_d t) + \frac{\sigma}{\omega_d}e^{-\sigma t}\sin(\omega_d t)$

步骤 4：合并三角函数项（三角恒等式）

将逆变换结果代入$V_{\text{out}}(t)$：

$v_{\text{out}}(t) = 1 - \left[ e^{-\sigma t}\cos(\omega_d t) + \frac{\sigma}{\omega_d}e^{-\sigma t}\sin(\omega_d t) \right]$

提取公因子$e^{-\sigma t}$，并利用 三角恒等式 合并正弦 / 余弦项：

设$A\cos x + B\sin x = C\sin(x + \theta)$，其中：

• 幅度$C = \sqrt{A^2 + B^2} = \sqrt{1 + \left( \frac{\sigma}{\omega_d} \right)^2} = \frac{1}{\sqrt{1-\zeta^2}}$（因$\sigma = \zeta\omega_0$，$\omega_d = \omega_0\sqrt{1-\zeta^2}$，故$\frac{\sigma}{\omega_d} = \frac{\zeta}{\sqrt{1-\zeta^2}}$）；
• 相位$\theta = \arccos\zeta$（因$\cos\theta = \zeta$，$\sin\theta = \sqrt{1-\zeta^2}$，满足$\cos x + \frac{\zeta}{\sqrt{1-\zeta^2}}\sin x = \frac{1}{\sqrt{1-\zeta^2}}\sin(\omega_d t + \theta)$）。

步骤 5：最终时域表达式

代入$\sigma = \zeta\omega_0$、$\omega_d = \omega_0\sqrt{1-\zeta^2}$ 和$\theta = \arccos\zeta$，得：

$v_{\text{out}}(t) = 1 - \frac{1}{\sqrt{1-\zeta^2}} e^{-\zeta\omega_0 t} \sin(\omega_d t + \arccos\zeta)$

附录：部分分式分解的系数推导

通分后分子为：

$A(s^2 + 2\zeta\omega_0 s + \omega_0^2) + s(Bs + C) = (A + B)s^2 + (2\zeta\omega_0 A + C)s + A\omega_0^2$

与原式分子$\omega_0^2$ 比较，系数需满足：

• 二次项：$A + B = 0$ →$B = -A = -1$（因$A=1$）；
• 一次项：$2\zeta\omega_0 A + C = 0$ →$C = -2\zeta\omega_0$；
• 常数项：$A\omega_0^2 = \omega_0^2$ → 恒成立（$A=1$）。

以上推导完整衔接了 拉普拉斯域→时域 的转换，核心利用 部分分式、复根配方、三角恒等式，最终得到欠阻尼（ζ<1）下的阶跃响应表达式。

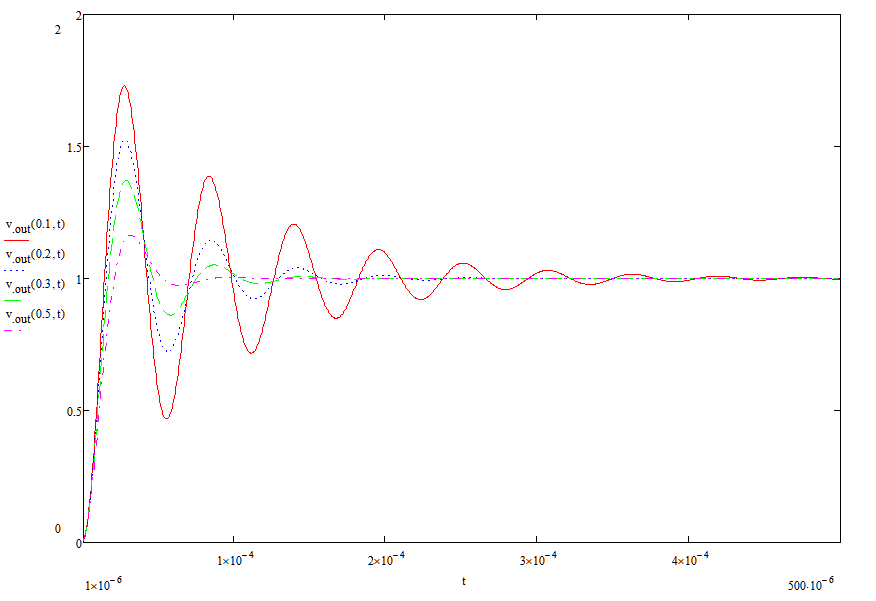
使用mathcad计算：