AI摘要:本文介绍了Green函数在超声物理中的应用,详细阐述了Green函数的物理意义、求解步骤和验证过程。Green函数描述了点源在特定位置产生的场,通过已知格林函数和源分布,可以计算出系统在源作用下的输出。文章首先从波动方程出发,通过时间谐波假设简化为亥姆霍兹方程,然后利用球对称性将方程降阶为常微分方程。接着求解齐次方程,并通过Dirac δ函数的积分性质确定常数。最后验证解满足原始非齐次波动方程,得出自由空间Green函数的表达式。
Powered by AISummary.
超声——Green函数的应用
物理上描述点源与其所产生的场之间的关系,可以使用Green函数求解。它们统一表示为:
$u(x)=\int\phi(\xi)G(\xi,x)d\xi$
对线性算子L,在点源δ作用下的输出(或响应)就是格林函数G,即:LG=δ。对于
声波波动问题,线性算子为:$L=\frac{\partial^2 }{\partial t^2} -c^2\Delta^2$
格林函数妙处在于若已知格林函数与源分布(包括时间上与空间上),则可通过格林函数与源的卷积求得在此源作用下系统的输出(或响应)。郭敦仁先生曾讲:“从物理上看,一个数理方程表示一种特定的场和产生这种场的源之间的关系(如热传导方程表示温度场和热源的关系),而格林函数则代表了一个点源所产生的场。知道了一个点源的场,就可以用叠加的方法算出任意源的场。”1
推导:已知:$L\varphi = Q$,其中 $L$ 是线性算子,$Q$ 为源分布,$\varphi$ 为待求输出。利用卷积的性质,可得:$\varphi = \varphi * \delta = \varphi * (LG) = (L\varphi) * G = Q * G$。(注:卷积的实质就是把所有源的作用都通过积分叠加起来)
已知的是源,G为格林函数,而格林函数无法直接求得。以下不同算子L对应的格林函数:
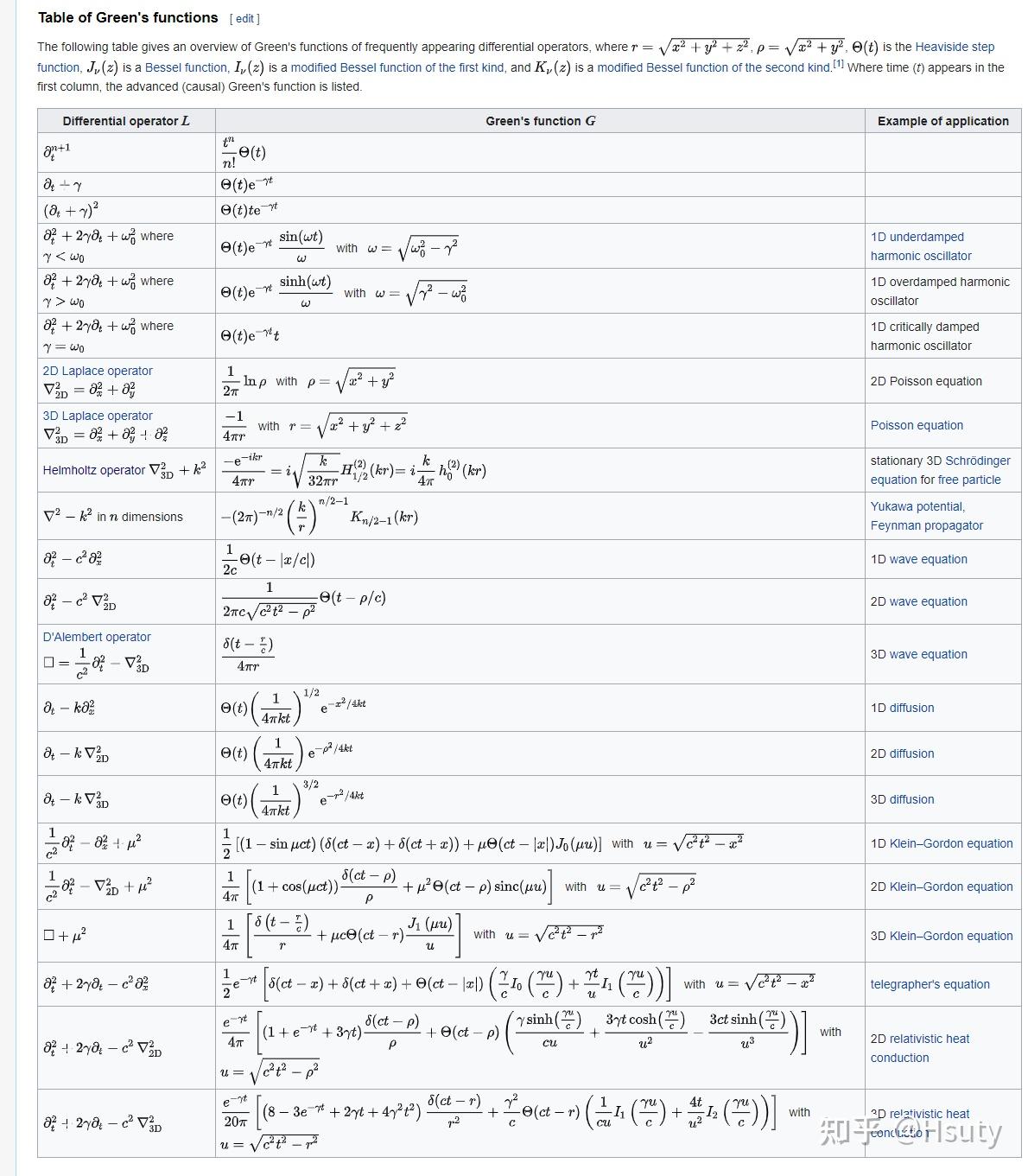
对于自由空间点声源,其相当于球源,但是点声源的半径r<<λ,故声压为:
$p=j\frac{\rho_0C_0kQ}{4\pi r}e^{j(wt-kr)}$
对于自由空间中,从$\overrightarrow{r} $到$\overrightarrow{r_0} $的声压为:
$p(\overrightarrow{r},\overrightarrow{r_0})=j\frac{\rho_0C_0kQ}{4\pi (\overrightarrow{r}-\overrightarrow{r_0})}e^{j(wt-k(\overrightarrow{r}-\overrightarrow{r_0}))}$
上式可以用Green函数表示,其中源函数Q为:$Q=Ae^{jwt}$
可知:$A=j\rho_0C_0kQ$
则声压可表示为:
$p(\overrightarrow{r},\overrightarrow{r_0})=Q*G=(j\rho_0C_0kQ)e^{jwt}G(\overrightarrow{r},\overrightarrow{r_0})$
其中格林函数G为:
$G(\overrightarrow{r},\overrightarrow{r_0})=\frac{1}{4\pi (\overrightarrow{r}-\overrightarrow{r_0})}e^{[-jk(\overrightarrow{r}-\overrightarrow{r_0})]}$
通过豆包AI,推导该格林函数。
波动方程的基本形式
在自由空间中,标量波动方程的一般形式为:
$$\nabla^2 \varphi - \frac{1}{c^2} \frac{\partial^2 \varphi}{\partial t^2} = -Q$$
对于单色波(时间谐波),假设场量具有时间依赖关系 $\exp(j\omega t)$,即 $\varphi(\vec{r}, t) = \varphi(\vec{r}) \exp(j\omega t)$($\omega$ 为角频率,$c$ 为光速 )。代入波动方程,利用 $k = \omega/c$($k$ 为波数 ),可简化为 亥姆霍兹方程(Helmholtz equation):
$$\nabla^2 \varphi + k^2 \varphi = -Q$$
(省略时间因子 $\exp(j\omega t)$,聚焦空间部分分析 )
Green 函数的物理意义
Green 函数 $G(\vec{r}, \vec{r}_0)$ 描述:源点 $\vec{r}_0$ 处点源在观察点 $\vec{r}$ 产生的场。需满足非齐次亥姆霍兹方程:
$$\nabla^2 G(\vec{r}, \vec{r}_0) + k^2 G(\vec{r}, \vec{r}_0) = -\delta(\vec{r} - \vec{r}_0)$$
其中 $\delta(\vec{r} - \vec{r}_0)$ 是三维 Dirac $\delta$ 函数,表示 $\vec{r} = \vec{r}_0$ 处的点源。
求解 Green 函数的步骤
(1) 利用球对称性简化问题
自由空间具有球对称性,设观察点与源点的相对位置矢量为 $\vec{R} = \vec{r} - \vec{r}_0$,模长 $R = |\vec{r} - \vec{r}_0|$。此时 Green 函数可表示为 $G(R)$(仅与 $R$ 有关 )。
球坐标系下,Laplacian 算子 $\nabla^2$ 简化为:
$$\nabla^2 = \frac{1}{R^2} \frac{d}{dR} \left( R^2 \frac{d}{dR} \right)$$
代入 Green 函数方程,得到:
$$\frac{1}{R^2} \frac{d}{dR} \left( R^2 \frac{dG}{dR} \right) + k^2 G = -\delta(R)$$
(2) 分析 $R \neq 0$ 的区域
当 $R \neq 0$ 时,$\delta(R) = 0$,方程退化为 齐次亥姆霍兹方程:
$$\frac{d^2 G}{dR^2} + \frac{2}{R} \frac{dG}{dR} + k^2 G = 0$$
这是球 Bessel 方程,其通解形式多样。但自由空间中,场需表示为向外传播的球面波(外行波),因此取推迟势(retarded potential) 形式:
$$G(R) = \frac{A}{R} \exp(-jkR)$$
($A$ 为待定常数,$\exp(-jkR)$ 描述外行球面波 )
(3) 利用 Dirac $\delta$ 函数确定常数 $A$
为确定 $A$,需利用 Dirac $\delta$ 函数的积分性质。在包含源点 $\vec{r}_0$(即 $R = 0$ )的小球(半径 $a$ )内积分 Green 函数方程:
$$\iiint_{V} \left( \nabla^2 G + k^2 G \right) dV = \iiint_{V} -\delta(\vec{r} - \vec{r}_0) dV = -1$$
利用格林第二恒等式,左边 Laplacian 项可转换为面积分:
$$\iiint_{V} \nabla^2 G dV = \oiint_{S} \nabla G \cdot d\vec{S}$$
($S$ 为小球表面,$d\vec{S} = a^2 \hat{R} d\Omega$,$\hat{R}$ 为径向单位矢量,$d\Omega$ 为立体角元 )
计算梯度 $\nabla G$:
$$\nabla G = \frac{dG}{dR} \hat{R} = A \left( -\frac{1}{R^2} \exp(-jkR) - \frac{jk}{R} \exp(-jkR) \right) \hat{R}$$
在小球表面 $S$($R = a$ )积分:
$$\oiint_{S} \nabla G \cdot d\vec{S} = A \oiint_{S} \left( -\frac{1}{a^2} \exp(-jka) - \frac{jk}{a} \exp(-jka) \right) a^2 d\Omega$$
由于 $\oiint_{S} d\Omega = 4\pi$(立体角积分),且当 $a \to 0$ 时,$\exp(-jka) \approx 1$、$ka \to 0$,上式简化为:
$$\oiint_{S} \nabla G \cdot d\vec{S} \approx -4\pi A$$
忽略高阶小量 $k^2 G$(当 $a \to 0$ 时可忽略 ),结合积分方程:
$$-4\pi A = -1 \implies A = \frac{1}{4\pi}$$
(4) 自由空间 Green 函数的形式
将 $A = \frac{1}{4\pi}$ 代入通解,得到:
$$G(\vec{r}, \vec{r}_0) = \frac{1}{4\pi |\vec{r} - \vec{r}_0|} \exp\left( -jk |\vec{r} - \vec{r}_0| \right)$$
验证 Green 函数满足波动方程
(1) 当 $\vec{r} \neq \vec{r}_0$($R \neq 0$ )时
此时 $\delta(\vec{r} - \vec{r}_0) = 0$,需验证 $\nabla^2 G + k^2 G = 0$。由于求解时已假设 $R \neq 0$ 满足齐次亥姆霍兹方程,因此自然成立。
(2) 当 $\vec{r} = \vec{r}_0$($R = 0$ )时
利用 Dirac $\delta$ 函数的定义:
$$\iiint_{V} \delta(\vec{r} - \vec{r}_0) dV = 1 \quad (\text{若 } \vec{r}_0 \in V)$$
Green 函数在 $R = 0$ 处的奇异性($G \propto \frac{1}{R}$ ),保证了方程右边的 $-\delta(\vec{r} - \vec{r}_0)$,验证成立。
总结
自由空间 Green 函数的推导步骤:
- 从波动方程出发,通过时间谐波假设简化为亥姆霍兹方程;
- 利用球对称性将方程降阶为常微分方程;
- 求解齐次方程并通过 Dirac $\delta$ 函数的积分性质 确定常数;
- 验证解满足原始非齐次波动方程。
最终,自由空间 Green 函数的表达式为:
$$\boxed{G(\vec{r}, \vec{r}_0) = \frac{e^\left( -jk |\vec{r} - \vec{r}_0| \right)}{4\pi |\vec{r} - \vec{r}_0|}}$$

