AI摘要:本文介绍了反激电路中Snubber电路的作用和设计方法。在没有Snubber电路的情况下,MOS管关断时会产生很大的过冲电压,可能导致MOS管损坏。通过使用RCD电路,可以吸收这些尖峰,降低峰值,保护MOS管。文章详细分析了MOS管导通和关断时的电压和电流变化,并提供了计算RCD参数的方法。最后,文章给出了参数确定的步骤和经验值,帮助设计者选择合适的RCD参数。
Powered by AISummary.
反激电路Snubber电路
使用Ltspice进行仿真,并进行说明,如下图所示为基本Flyback电路。
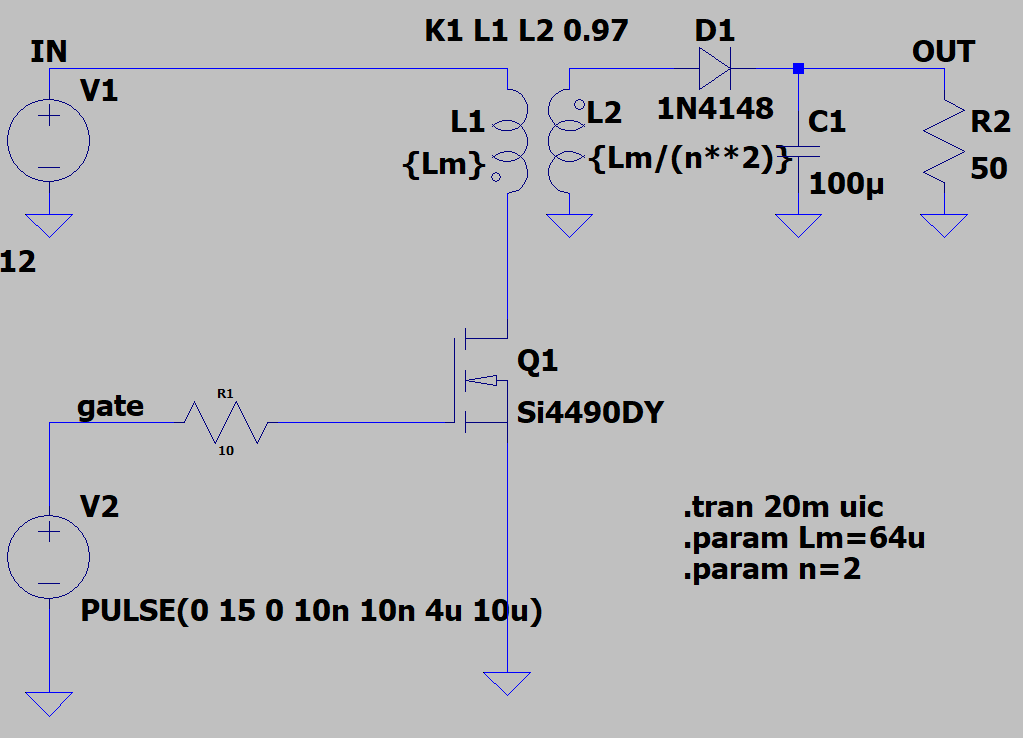
上图电路中没有任何snubber电路,Q1 MOS的D极在关断时会产生很大的过冲。如下图所示。
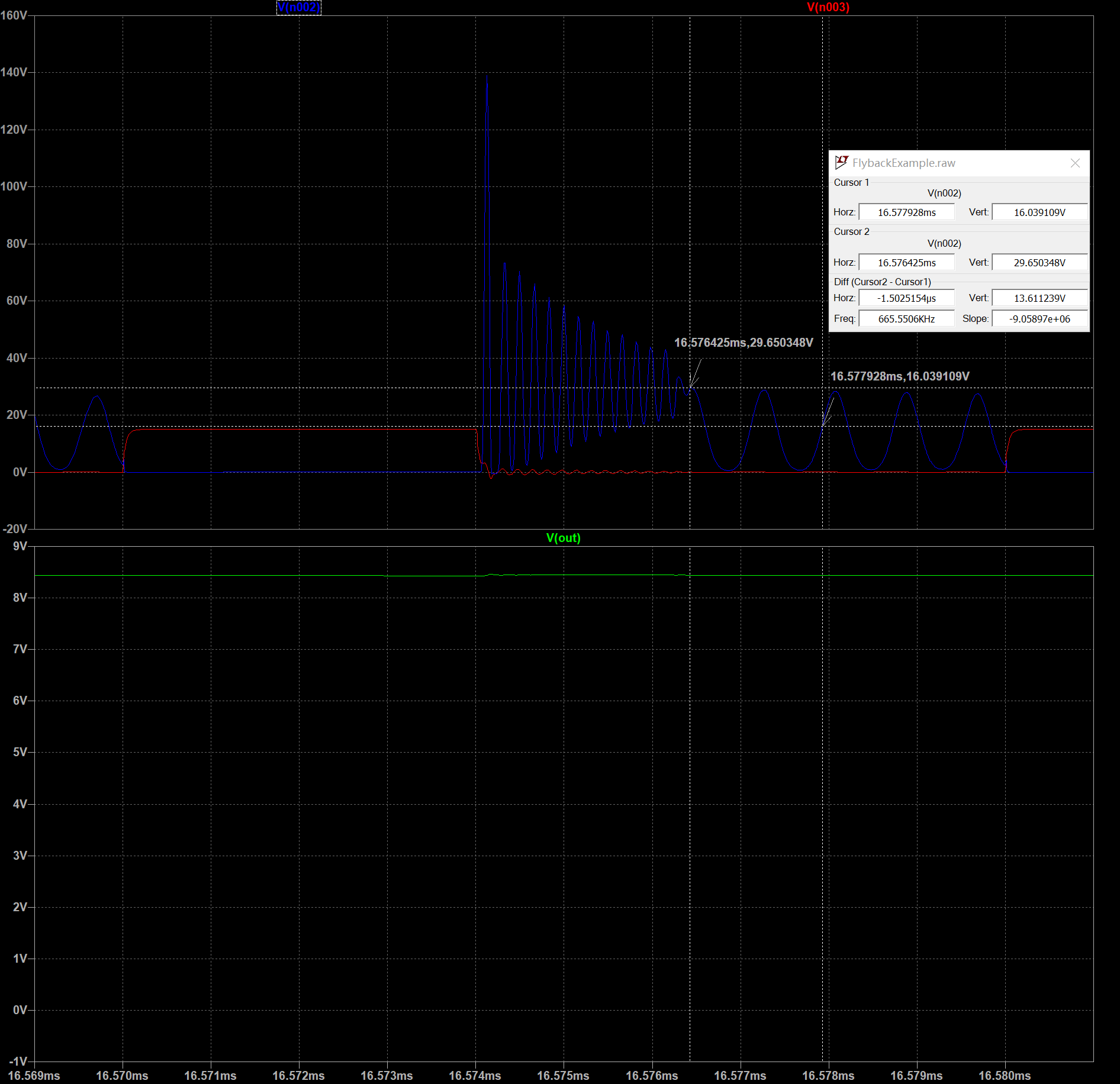
当没有RCD电路时,在MOS管关断瞬间的电压和电流可以做如下简单分析。
假设漏感为Llk,MOS关断时阻抗R可等效为∞,根据KVL单独计算漏感产生的电压和电流。由于MOS导通时电源给漏感储能,故这时候由漏感放电。
漏感电压为:
$V_{lk}=L_{lk}\frac{di_{lk}}{dt}$
R两端电压为Vlk,电流为:
$i_{lk}=\frac{V_{lk}}{R}$
联立2式为:
$V_{lk}=L_{lk}\frac{d(\frac{V_{lk}}{R})}{dt}=L_{lk}\frac{dV_{lk}}{Rdt}$
$\frac{R}{L_{lk}}dt=\frac{dV_{lk}}{V_{lk}}$
两边求积分,得
$\frac{R}{L_{lk}}t=ln(V_{lk})$
$V_{lk}=e^{\frac{R}{L_{lk}}t}$
电流为:
$i_{lk}=\frac{V_{lk}}{R}=\frac{e^{\frac{R}{L_{lk}}t}}{R}$
一般性的,假设R=10MΩ,时间t为瞬间为1ps,电感为1uH,则有:
Vlk=22kV,Ilk=0.0022A
可见此时MOS管关断瞬间,DS两端电压很高,漏感电流瞬间变为接近0。电感电流瞬间变化到0必然导致电压升高到无穷大。
仿真结果中,第1个脉冲达到了140V左右,这个就是漏感瞬间断电时导致电压突变。
这就需要使用RCD电路将这些尖峰吸收掉,降低这些峰值,防止MOS过压损坏。
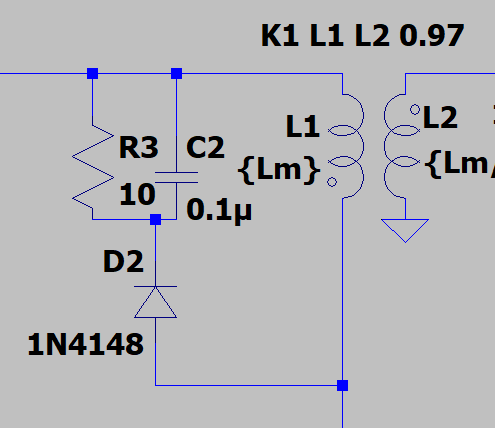
第1阶段
MOS管导通时,电源给变压器充电,由于次级二极管反向,没有电流回路,故初级是漏感和励磁电感储存能量。电感的充电公式为:$V=L\frac{di}{dt}$
对其求积分为:$i=\frac{V}{L}t$,这说明电感的电流是随时间直线上升的,上升斜率为$\frac{V}{L}$。电感电流不能突变,只能直线上升,而电感两端的电压是不变的。但现实是电感是有内阻DCR,如果考虑电感内阻,则电流不会一直上升。
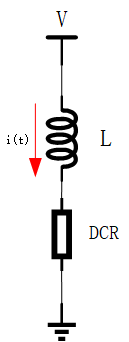
$V=L\frac{di}{dt}+iR$
$\frac{di}{V-iR}=\frac{dt}{L}$
两端求积分为:$\frac{t}{L}=-\frac{1}{R}ln(V-iR)$,时间从0开始计算为:$\frac{t}{L}=-\frac{1}{R}ln(V-IR)-[-\frac{1}{R}ln(V)]$
$-\frac{R}{L}t+ln(V)=ln(V-IR)$
$ln(Ve^{-\frac{R}{L}t})=ln(V-IR)$
$V-IR=Ve^{-\frac{R}{L}t}$
$I=\frac{V}{R}(1-e^{-\frac{R}{L}t})$
内阻DCR两端电压为:$V_R=V(1-e^{-\frac{R}{L}t})$,其波形如下图所示。
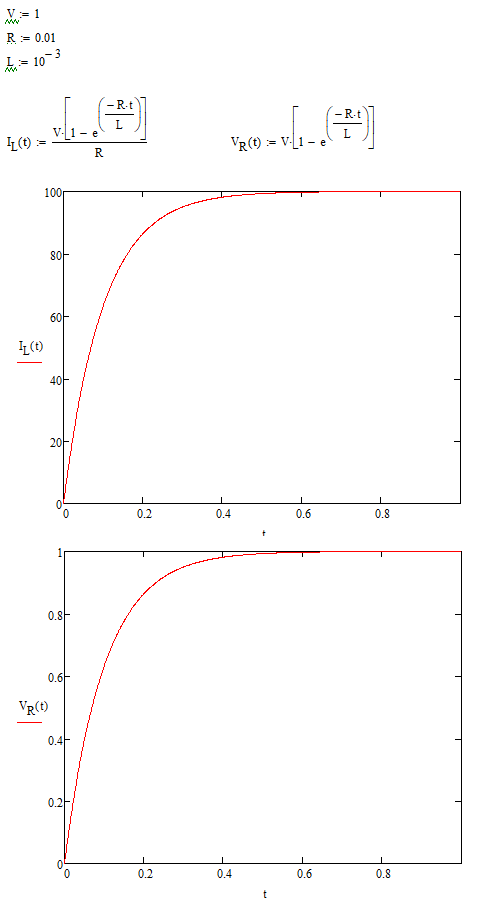
当忽略内阻时,则是直线上升。以下为仿真(有RCD电路)结果。
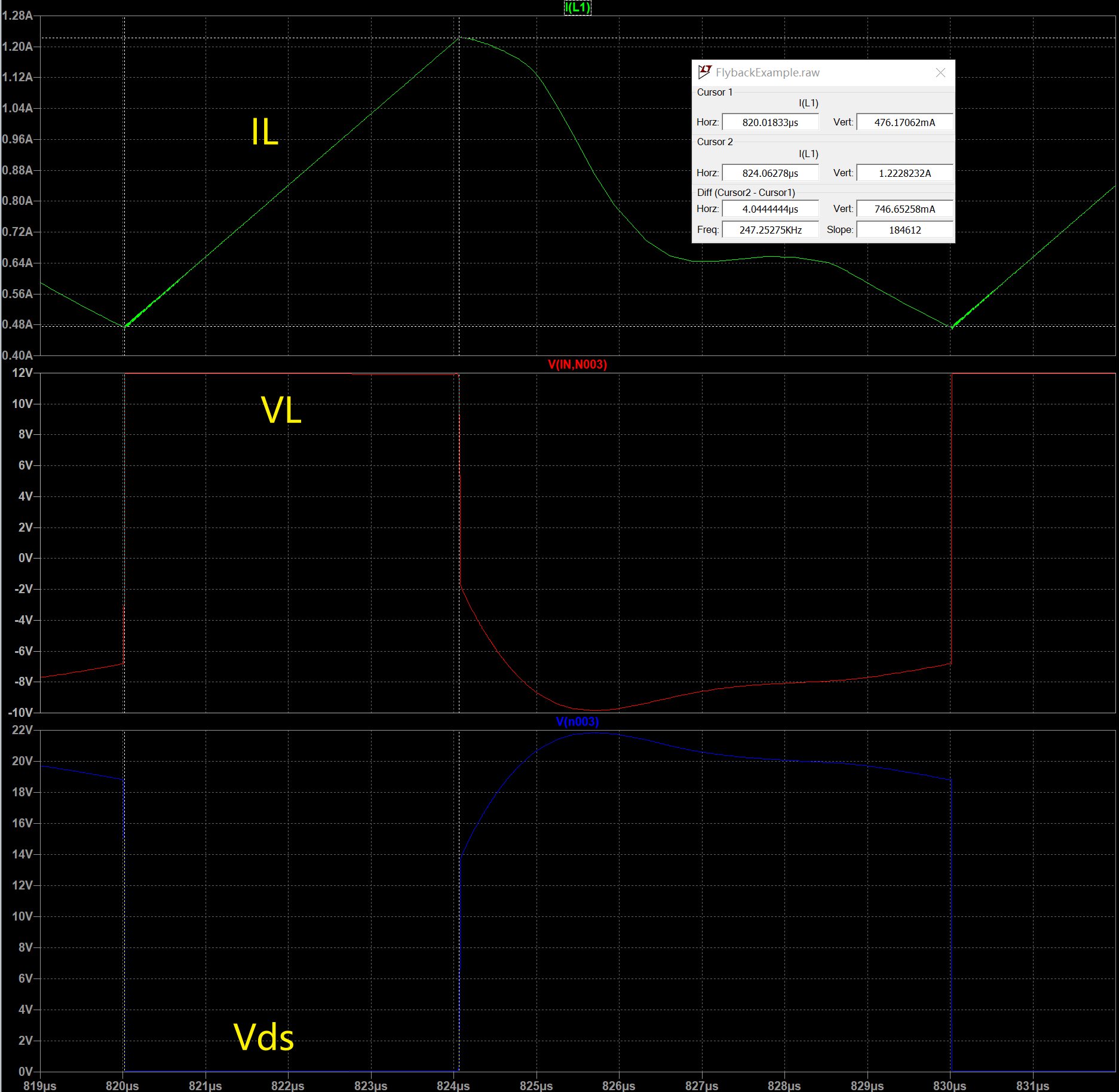
第2阶段
当MOS管关断瞬间,D极电压相当于无穷大电阻进行了分压,此时D极电压为Vin。然后漏感和励磁电感反向放电,励磁电感放电通过变压器给负载供电,此时励磁电感两端电压与输出电压成匝数比n倍的关系。而漏感不参与变压器输出,作为额外的存能元件放电,会将D极电压进一步抬高,当电压高于某个电压时,二极管导通,形成回路,漏感开始放电。
在没有RCD电路的情况下,如下图所示。
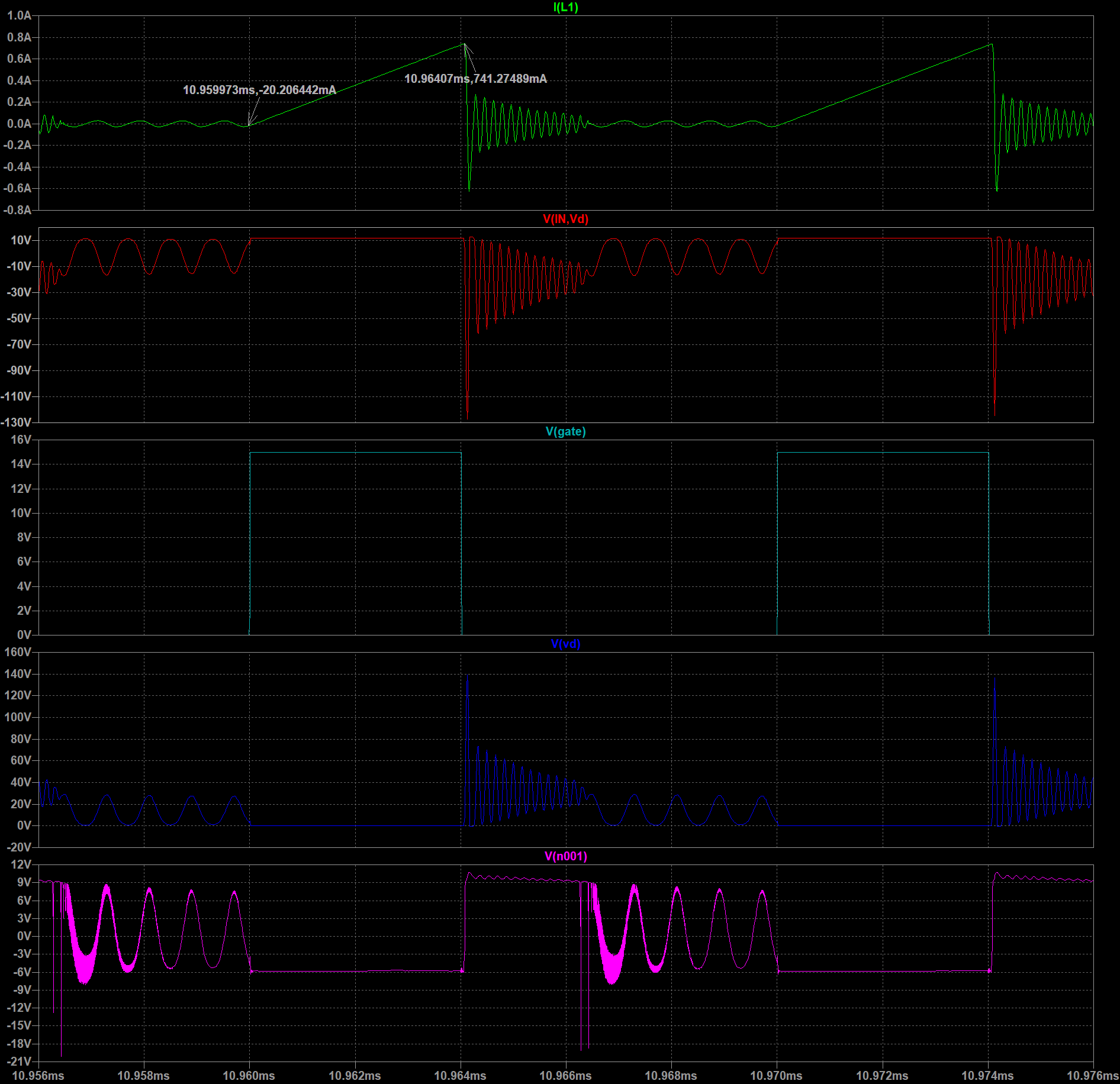
当MOS关断瞬间,线圈电感和Coss形成振荡,D极产生极大的脉冲电压,当一端时间稳定后,D极电压为nVo+Vin左右。
当加入RCD电路后,如下图所示。
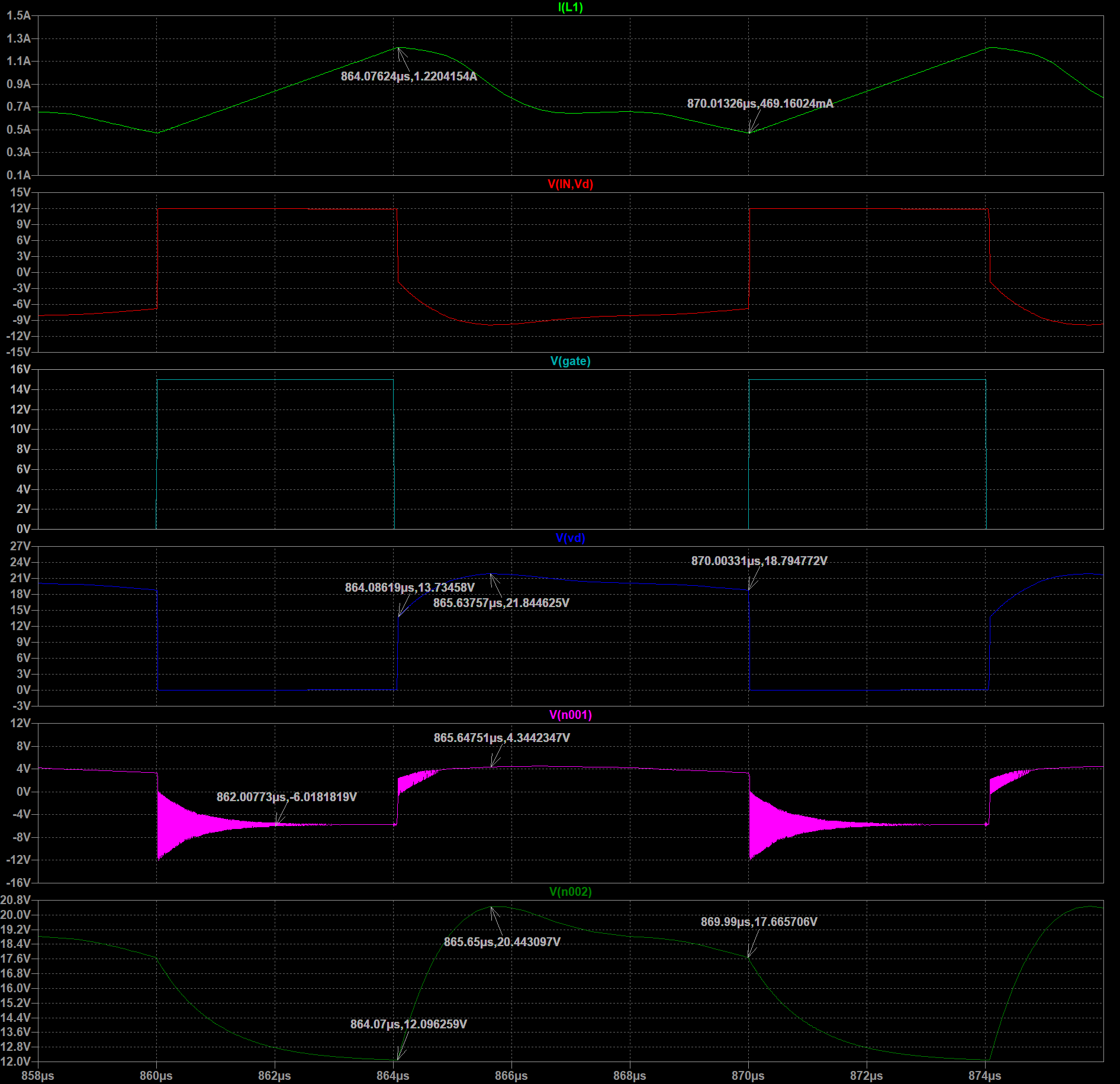
当D极电压因为电感与Coss的振荡上升到高于Vin时,RCD的二极管D导通,开始给电容充电,同时变压器的电感电流下降,给电容充电变缓慢,达到峰值后电容电压下降。
这里存在3个电源:电源Vin,副边反射到原边的电压nVout,漏感放电产生的电压Vlk。
根据KVL计算每个电源在MOS D极的电压,然后求和就是D极的总电压。
电源Vin对D极
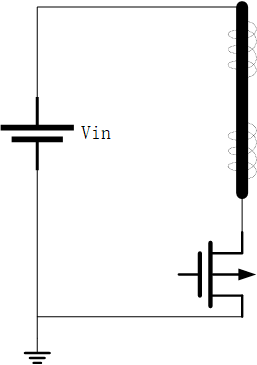
根据KVL,其他2个电源为短路,则D极电压就是电源电压Vin。
副边反射电压对D极
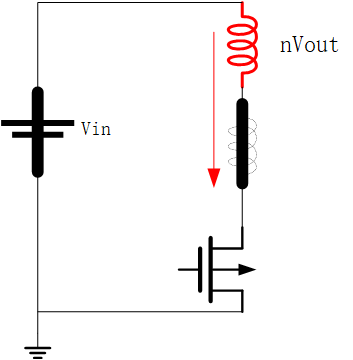
根据KVL,电源Vin为短路,漏感也是短路。副边电压为上正下负,反射到原边为下正上负,故D极电压为nVout。
漏感对D极
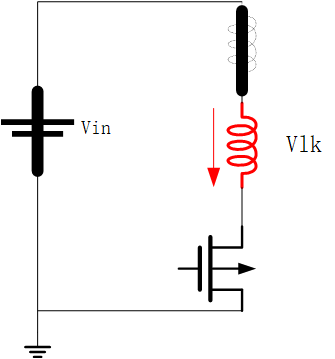
同上,漏感对D极产生的电压为Vlk。
$V_{lk}=L_{lk}\frac{di_{lk}}{dt}$
由上可知关断后D极电压为:$V_d=V_{in}+nV_{out}+V_{lk}$
当RCD的二极管导通时,忽略二极管导通电压,漏感产生的电流会通过RCD电路给电容充电。
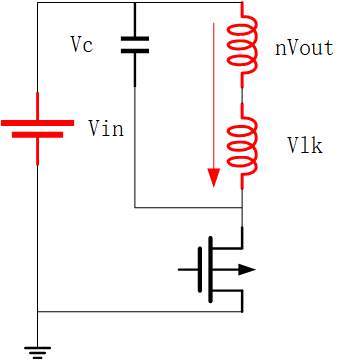
此时电容两端的电压就是副边反射电压和漏感电压之和,即:$V_c=nV_{out}+V_{lk}$
最高电压就是RCD钳位电压Vc(也是电容C两端的电压)和Vin的和,即$V_d=V_{in}+nV_{out}+V_{lk}=V_{in}+V_c$1。
由于D极电压一直高于Vin,所以这个过程过程中R不会消耗C中存储的电流,在关断的时间toff内,电容电压会上升到Vc,同时漏感电流也会减小,漏感和RCD电路会达到一个振荡平衡,导致电容电压保持在Vc。
只有当MOS导通时,Vd=0V时,RCD的二极管关断,这时C中存储的电流就会通过R释放掉。故在MOS关断这个过程中,由漏感、RCD构成回路进行充放电。
其中漏感电压为流过线圈电流的微分,即:$V_{lk}=L_{lk} \frac{di_{lk}}{dt}=L_{lk} \frac{\Delta i_{lk}}{\Delta t}$,$\Delta i_{lk}$为开关导通时漏感充电电流上升的最大值,在开关关断时会放电。
RCD流入的电流存储在电容中,然后在MOS导通时消耗掉。故流入RCD电容的平均电流与消耗在RCD电阻上的电流相同。电阻两端电压为Vc,则电流为:$i_{D}=\frac{V_c}{R}$
由于漏感产生的电流是流入到RCD中电容,故漏感在该过程中的平均电流也是iD,即:$i_D=\frac{1}{2}\frac{\Delta i_{lk} \Delta t}{Ts}$,其中Ts为开关周期。
联合以上式子可得:$V_c-nV_{out}=V_{lk}=L_{lk}\frac{\Delta i_{lk}}{\Delta t}$
则:$\Delta t=\frac{L_{lk}\Delta i_{lk}}{V_c-nV_{out}}$
$i_D=\frac{V_c}{R}=\frac{1}{2}\frac{\Delta i_{lk} \frac{L_{lk}\Delta i_{lk}}{V_c-nV_{out}}}{Ts}=\frac{1}{2T_s}\frac{L_{lk} \Delta i_{lk}^2}{V_c-nV_{out}}$
漏感在整个开关周期Ts内的能量为:$W_{lk}=\frac{1}{2}L_{lk}\Delta i_{lk}^2$,则整个开关周期内的功率为:$P_{lk}=\frac{W_{lk}}{Ts}=\frac{1}{2}L_{lk}\Delta i_{lk}^2 f_s$
在整个开关周期Ts内,只有MOS导通时RCD电阻有消耗,其功率为:$P_{R}=V_c*i_D=V_c*\frac{1}{2T_s}\frac{L_{lk} \Delta i_{lk}^2}{V_c-nV_{out}}=P_{lk}\frac{V_c}{V_c-nV_{out}}=P_{lk}\frac{1}{1-\frac{nV_{out}}{V_c}}$
定义:$k=\frac{V_c}{nV_{out}}$
则有:$\xi=\frac{P_R}{P_{lk}}=\frac{1}{1-\frac{1}{k}}=\frac{k}{k-1}$
$V_d=V_{in}+(k+1)V_c$
可以做出Vd和ζ关于k的归一化图,蓝色为ζ,红色为Vd。
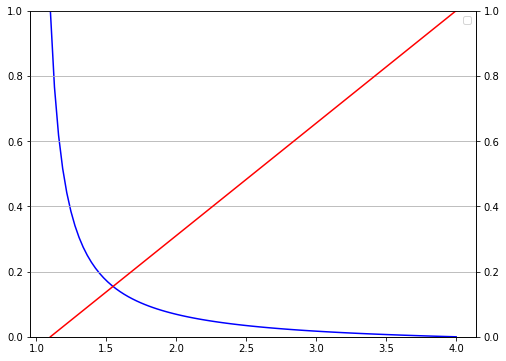
根据经验,k取值范围为:1.5~3。
参数确定
首先确定Vin最大值和选择的MOS管的Vds最大电压,预留的电压余量Vmargin。则Vc为:$V_{ds_(max)}-V_{margin}-V_{in_(max)}$
然后确定k为3或者其他,则可以算出反射电压:$nV_{out}=\frac{V_c}{k}$
根据Vout最小值,可以算出:$n=\frac{V_c}{kV_{out}}$
电阻的功率为Pr,则电阻为:$R=\frac{V_c^2}{P_R}=\frac{V_c^2}{P_{lk}}(1-\frac{1}{k})$
Plk可以根据无RCD时测量的Ilk峰值和原边漏感计算出来。
RCD的电容需要充放电,电容的功率为:$P_c=\frac{1}{2}C \Delta V_c^2f_{s}$,电容的功率最终全部消耗在电阻R上。
增大电容可以降低振荡电压,但也会增加功耗。

