AI摘要:电流互感器是一种用于测量电流的设备,其原理是通过罗尔线圈形式降低对负载的影响,并利用匝数比放大感应电压。设计电流互感器时,需要考虑减小检测电阻、增加副边激磁电感、增加线圈匝数和提高磁导率等措施以提高精度。设计步骤包括设定检测电压范围、计算副边电流、确定匝数比、选择磁芯和线材、计算铜损和估算磁损。
Powered by AISummary.
电流互感器
原理分析
电流互感器的等效电路如下图所示。
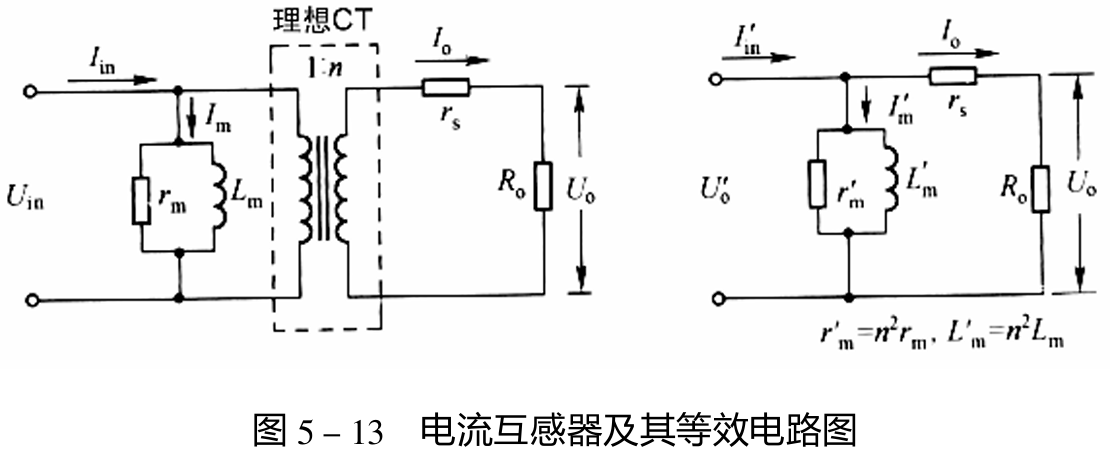
电流互感器是串在负载回路中的,为了降低对负载的影响,一般使用罗尔线圈形式,即一根线缆穿过磁环中心。再通过匝数比,将感应电压放大几十倍,方便后级电路处理。
线圈可以均匀分布在磁环上,可以忽略漏感。
副边接检测电阻R,将电流信号转换为电压信号。
| 名称 | 定义 |
|---|---|
| Iin | 待测电流 |
| Im | 激磁电流 |
| Io | 副边电流 |
| I‘in | Iin折算到副边电流 |
| I'm | Im折算到副边电流 |
| Lm | 激磁电感 |
| L'm | Lm折算到副边电感 |
| rm | 激磁电感电阻 |
| r’m | rm折算到副边电阻 |
| rs | 副边电阻 |
| Ro | 检测电阻 |
| Uin | 输入电压 |
| Uo | 输出电压 |
| N1 | 原边匝数 |
| N2 | 副边匝数 |
| n | 匝数比,1圈/n圈,即N1=1,N2=n |
$\frac{I_{in}-I_m}{n}=I_o$,则可知折算后的电流为:
$I_{in}'=\frac{I_{in}}{n}$
$I_{m}'=\frac{I_{m}}{n}$
$I_{in}'=I_m'+I_o$
副边电压为:$U_2=I_o(R_o+r_s)=K_ffN_2B_wA_e$,正弦波波形系数Kf=√2π=4.44。
$U_m'=I_m' \times jwL_m'=I_o \times (r_s+R_o)$
$I_{in}'=\frac{I_o \times (r_s+R_o)}{jwLm'}+I_o$
相位差为α,则$tan \alpha=\frac{(r_s+R_o)}{wLm'}$,$\alpha = arctan\frac{(r_s+R_o)}{wLm'}$
其中$L_m'=n^2L_m$
原边激磁电感为:$L_m=N_1^2 \mu_0 \mu_a A_e/l$
副边检测电流与原边检测电流的幅值相对误差为:$\xi=\frac{I_{in}'-I_o}{I_{in}'}=1-cos\alpha$
根据泰勒展开可得:$\xi=1-cos\alpha=\frac{\alpha^2}{2}$
根据上式,可知,要减少相对误差,则需要减小α。
- 减少rs+Ro,即减少检测电阻
- 增加Lm‘,即增加副边激磁电感
当副边激磁电抗远大于检测电阻时,即$wL_m'>>(r_s+R_o)$,则$I_m'<<I_o<I_{in}'$,一般情况下rs<<Ro
α可近似为:$\alpha=\frac{R_o}{wLm'}=\frac{R_o}{wn^2L_m}=\frac{R_o}{wn^2A_L}$
$\alpha = \frac{\frac{U_2}{I_o}}{wn^2L_m}=\frac{U_2}{wI_on^2N_1^2\mu_0 \mu_aA_e/l}=\frac{U_2}{wI_on^2N_1^2A_L}=\frac{U_2}{wI_on^2A_L}=\frac{U_2}{w(I_{in}-I_m)nA_L}$
$nA_L=\frac{U_2}{\alpha w (I_{in}-I_m) }=\frac{U_2}{ w (I_{in}-I_m) \sqrt{2\xi}}$
上式可以忽略Im,则为:
$nA_L=\frac{U_2}{ w I_{in} \sqrt{2\xi}}$
根据以上分析,提高精度的措施有:
- 减小Ro,增加Lm
- 增加线圈匝数n
- 提高磁导率u,减小损耗
当原边电流降低时,磁通密度成比例降低,但低磁通情况下,励磁安匝比磁通密度降低的要慢,这会导致误差增大。
设计步骤
- 设定检测电压范围Uo
- 设定检测电阻Ro,可选择几个参数进行计算
- 计算副边电流Io,Uo/Ro
- 根据原边电流Iin和以上计算匝数比n
- 根据$U_2=I_o(R_o+r_s)=K_ffN_2B_wA_e$计算Ae,选择磁芯
- 选择可以绕制的AWG线材
- 计算铜损
- 估算磁损

