AI摘要:无线充电技术基于空气变压器原理,通过线圈间的电磁感应实现能量传输。文章详细分析了无线充电的等效电路,包括空载和负载状态下的变压器模型,以及耦合系数对系统性能的影响。通过仿真和实验数据,探讨了谐振频率、输入阻抗和系统增益等关键参数。此外,还介绍了工程实践中的漏感测量方法和耦合电容对系统性能的影响。最后,文章提供了直接基于互感模型的仿真方法,并对比了不同模型的增益和频率特性。
Powered by AISummary.
无线充电原理
空载变压器等效电路
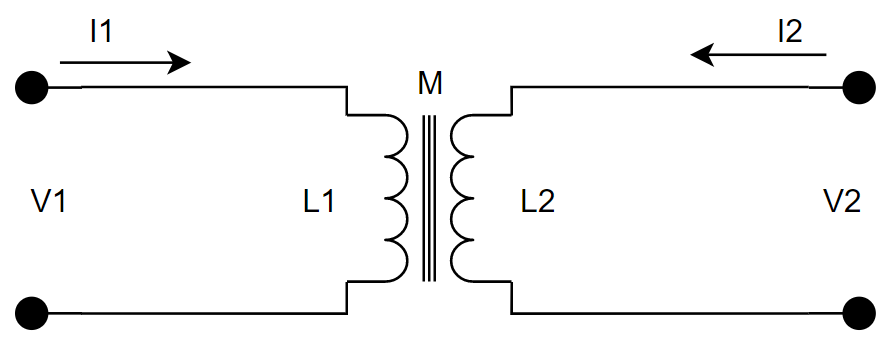
无线充电是一个空气变压器,铁心为空气Air的变压器。简化的耦合电路如上图所示。
- 线圈互感为M
- 原边线圈电感为L1,副边为L2
- 输入电压为V1,输入电流为I1
- 输出电压为V2,输出电流为I2
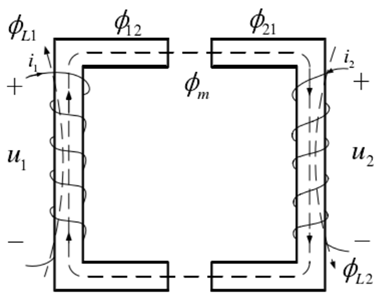
电流 $i_1$ 经过一次侧线圈产生磁通 $\phi_1$ , $\phi_1$ 中部分磁通泄漏出去,这部分为一次侧线圈的漏磁通 $\phi_{L_1}$ ,另外一部分经过空气气隙或者铁心到二次侧线圈,这部分为交链磁通 $\phi_{12}$ 。 $\phi_{12}$ 在二次侧线圈产生感应电流 $i_2$ ,电流经过线圈又产生磁通 $\phi_2$ ,$\phi_2$ 中也有部分磁通泄漏出去,为漏磁通 $\phi_{L_2}$ ,另外一部分经过空气气隙或者铁心到一次侧线圈,为交链磁通 $\phi_{21}$ 。
$i_1$ 产生的磁通为:$\phi_1=\phi_{12}+\phi_{L_1}$
$i_2$ 产生的磁通为:$\phi_2=\phi_{21}+\phi_{L_2}$
一次侧和二次侧产生的互磁通为:$\phi_m=\phi_{12}+\phi_{21}$
一次侧绕组和二次侧绕组交链产生的总磁通为一次侧电流产生的磁通和二次侧磁通到一次侧的交链磁通之和,这些都是一次侧电流产生的: $\phi_{\sigma_1}=\phi_1+\phi_{21}$
二次侧绕组的同理为: $\phi_{\sigma_2}=\phi_2+\phi_{12}$
则 $u_1$ 和 $u_2$ 为:
$u_1=N_1\frac{d\phi_{\sigma_1}}{dt}=N_1\frac{d\phi_m}{dt}+N_1\frac{d\phi_{L_1}}{dt}=L_m\frac{di_m}{dt}+L_{s_1}\frac{di_1}{dt}$
$u_2=N_2\frac{d\phi_{\sigma_2}}{dt}=N_2\frac{d\phi_m}{dt}+N_2\frac{d\phi_{L_2}}{dt}=\frac{N_2}{N_1}L_m\frac{di_m}{dt}+L_{s_2}\frac{di_2}{dt}$
$L_m$ 为励磁电感:$L_m=\frac{N_1\phi_{m}}{i_m}$
根据磁势平衡(安匝平衡,不考虑损耗),可知 $N_1i_1+N_2i_2=N_1i_m$
$i_m$为励磁电流:$i_m=i_0=i_1+i_2\frac{N_2}{N_1}$
$L_{s_1}$为一次侧漏电感:$L_{s_1}=N_1\frac{\phi_{L_1}}{i_1}$
$L_{s_2}$为一次侧漏电感:$L_{s_2}=N_2\frac{\phi_{L_2}}{i_2}$
一次侧电流 $i_1$ 产生的交链磁通 $\phi_{12}$ 在二次侧线圈上产生的等效电感为互感 $M_{12}$ : $M_{12}=N_2\frac{\phi_{12}}{i_1}$
同理,二次侧在一次侧线圈上产生的互感为 $M_{21}=N_1\frac{\phi_{21}}{i_2}$
$M_{12}=M_{21}=M=\frac{N_2}{N_1}L_m$
根据互感的原理1,可知
$u_1=N_1\frac{d\phi_{\sigma_1}}{dt}=N_1\frac{d\phi_1}{dt}+M\frac{di_2}{dt}=L_1\frac{di_1}{dt}+M\frac{di_2}{dt}$
$u_2=N_2\frac{d\phi_{\sigma_2}}{dt}=N_2\frac{d\phi_2}{dt}+M\frac{di_1}{dt}=L_2\frac{di_2}{dt}+M\frac{di_1}{dt}$
$L_1$为一次侧绕组自感:$L_1=N_1\frac{\phi_1}{i_1}$
$L_2$为二次侧绕组自感:$L_2=N_2\frac{\phi_2}{i_2}$
$L_{s_1}$为一次侧漏电感:$L_{s_1}=L_1-L_m$
$L_{s_2}$为一次侧漏电感:$L_{s_2}=L_2-L_m$
通常定义耦合系数k来表示一、二次绕组电磁耦合松紧程度,即表示两个线圈自感磁通链与互感磁通链的比值。
$k=\sqrt{\frac{\phi_{12}\phi_{21}}{\phi_1\phi_2}}=\sqrt{\frac{Mi_1Mi_2}{L_1i_1L_2i_2}}=\frac{M}{\sqrt{L_1L_2}}$
根据以上可得变压器得T形等效电路。
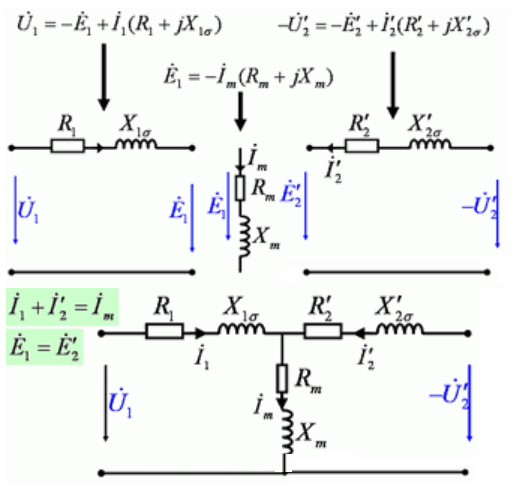
其中R1为一次侧绕组电阻,X1为一次侧绕组漏感,Xm为互感,Rm为互感电阻,R2‘为二次侧等效到一次侧得电阻,X2'为二次侧等效到一次侧得漏感,I2’为二次侧等效到一次侧得电流。它们得关系如下。
$i_2'=i_2\frac{N_2}{N_1}$
$R_2'=(\frac{N_2}{N_1})^2R_2$
$L_2'=(\frac{N_2}{N_1})^2L_2$
$U_2'=U_2\frac{N_1}{N_2}$
实际变压器等效模型可如下图所示。
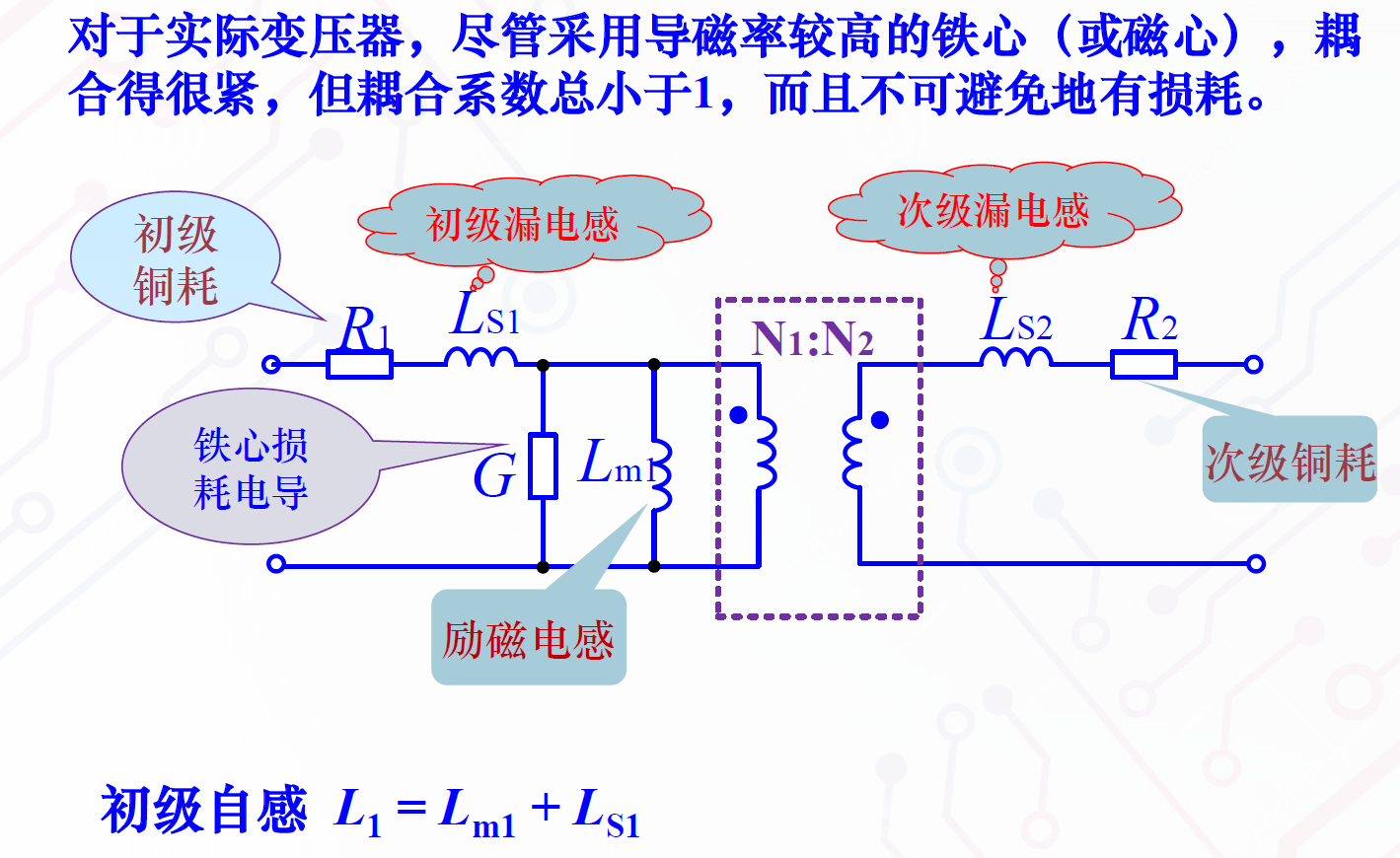
可以将上面的耦合模型中的次级漏感等效为0,变为下面的等效模型。
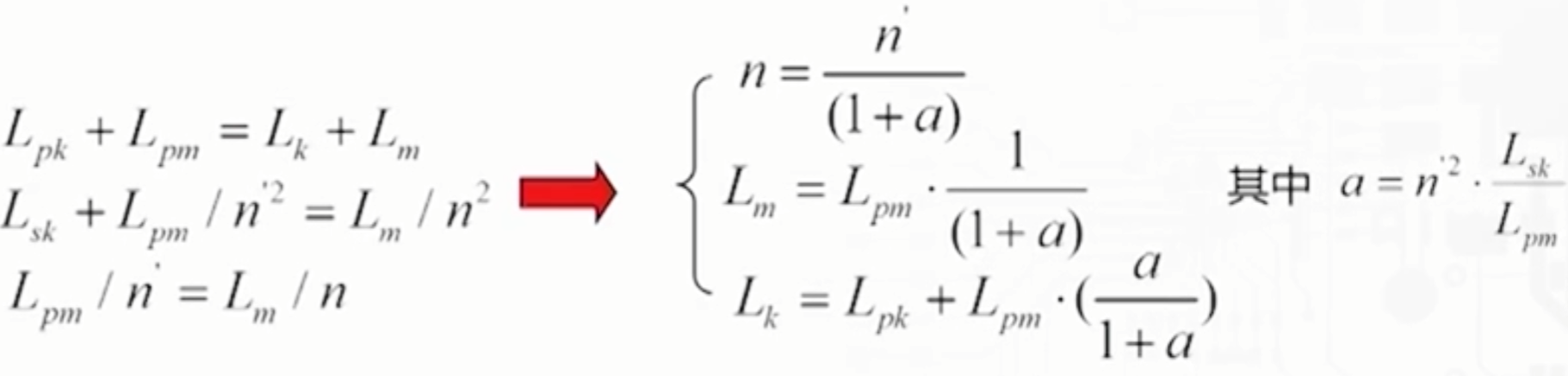
其中的n‘=N1:N2。
测量初级电感时,次级开路,电感为L1o,次级短路为L1s;测量次级电感时,初级开路为L2o,初级短路为L2s。等效关系式如下所示。

负载变压器等效电路
以下等效电路二次侧绕组电感和电阻未换算

以下等效电路二次侧换算到一次侧,这里面没有耦合系数。
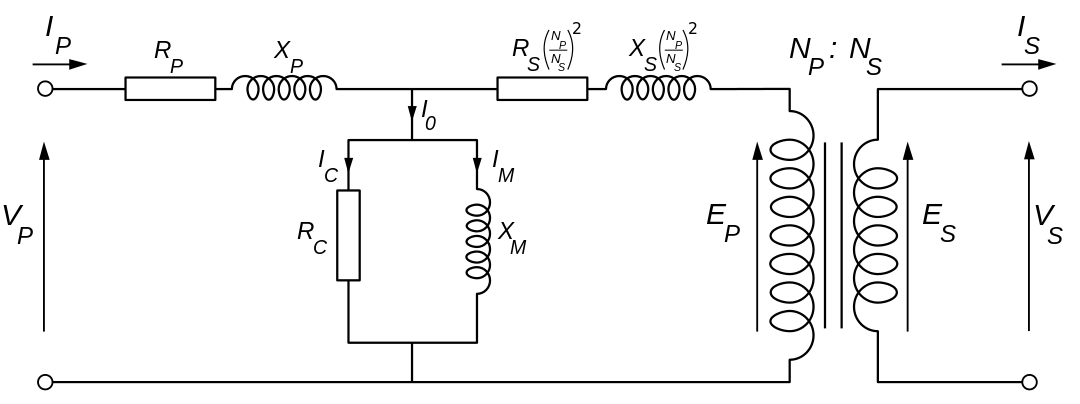
继续简化变为L形等效电路。
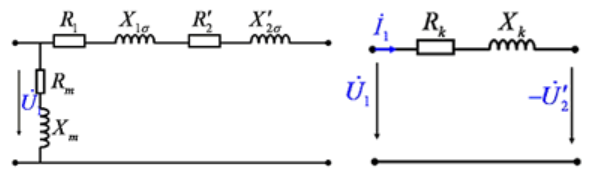
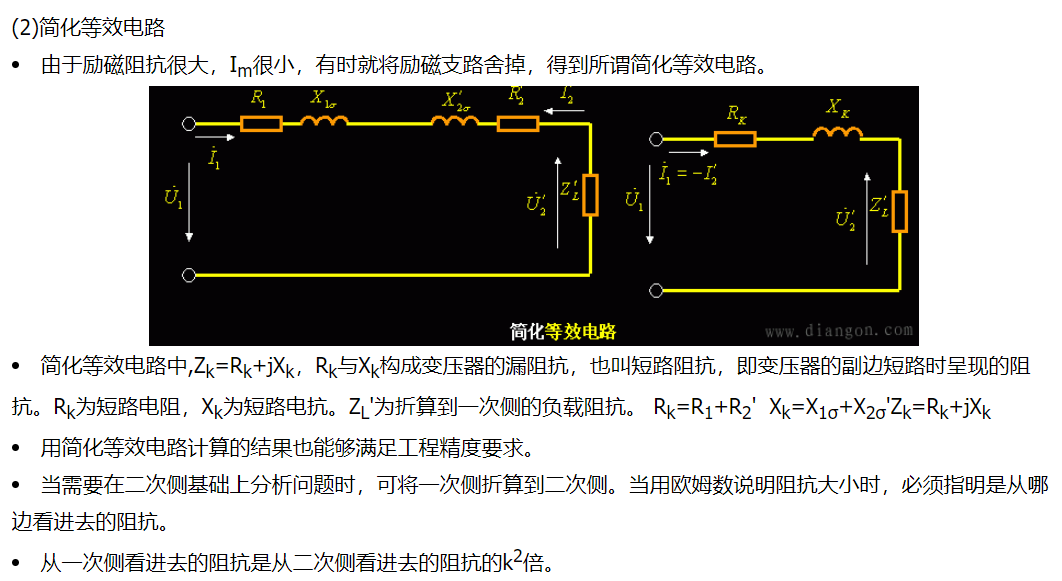

这里要注意,工程中的漏感是实验测试所得,与电气学会定义的漏感有所不同2。
以下是电气学会定义的漏感等效电路。
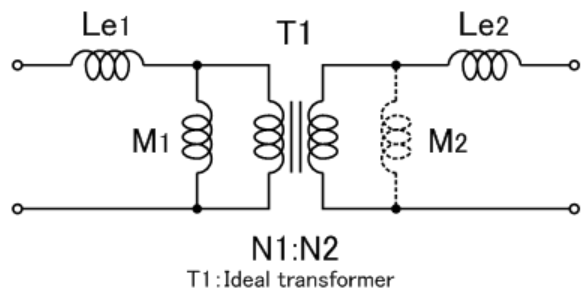
以下为工程中测量时所用模型。一般使用过程中,使用工程模型。这里面会忽略
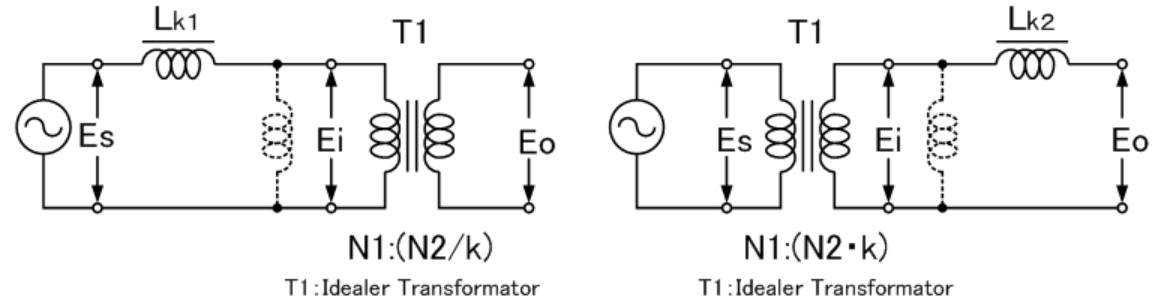
将次级侧短路测量初级侧所得的电感称为初级侧漏电感Lk1,将初级侧短路测量次级侧所得的电感称为次级侧漏电感Lk2。利用这些数值与各自的线圈的自感,算出的耦合系数k,在初级侧及次级侧所测量到的数值必须完全相同。
两互感线圈之间的电磁感应强度与M和L11、L22有关,同时与线圈之间的磁链耦合松紧度有关(比如线圈距离、偏心度等)。线圈之间的耦合强度使用k表示,称为“耦合系数”。这个L11和L22是耦合自感,是开路测量。
$k=\frac{M}{\sqrt{L_{11}L_{22}}}=\sqrt{1-\frac{L_{12}}{L_{11}}}=\sqrt{1-\frac{L_{21}}{L_{22}}}$
经过换算可得如下所示等效电路。
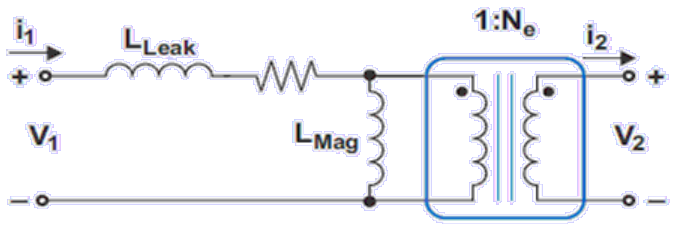
其中各式子为:
$L_{lk}=k^2L_{11}$
$L_m=(1-k^2)L_{11}$
$\frac{N_2}{N_1}=\sqrt{\frac{L_{22}}{L_{11}}}$
$N_e=\frac{N_1}{N_2k}=\frac{1}{k}\sqrt{\frac{L_{11}}{L_{22}}}$
L1、L12,L21、L2分别为3:
- L11:TX Coil电感@RX Coil 开路,初级侧线圈耦合自感
- L12:TX Coil电感@RX Coil 短路,初级侧线圈耦合漏感2
- L22:RX Coil电感@TX Coil 开路,次级侧线圈耦合自感
- L21:RX Coil电感@TX Coil 短路,次级侧线圈耦合漏感
这里测量的漏感是涵盖次级侧部分漏感,同样对于次级侧测量的漏感也是一样。故这里的漏感与纯粹的初级侧漏感不一样。电气学会的漏感是真实的单边漏磁通产生的等效电感,工程漏感除以(1+k)就是电气学会漏感。
无线充电等效电路
根据以上描述,无线充电或者空心变压器可以按照2种模型来等效。一种是按照电气学会的耦合系数标准等效的有初级和次级漏感,另一种是将次级漏感和自感全部等效,按照工程定义测量漏感和自感。
工程定义等效电路
将耦合电容加入等效电路中,如下图所示。
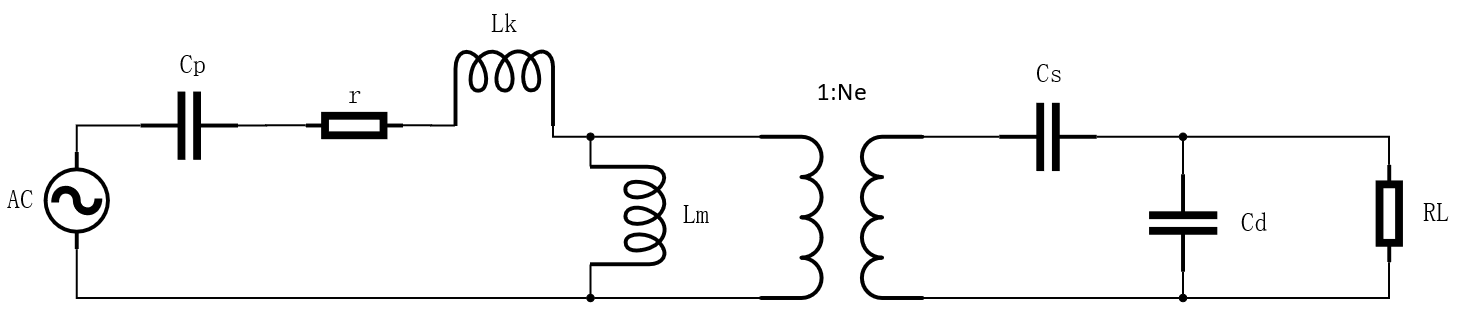
换算到一次侧则如下图所示。
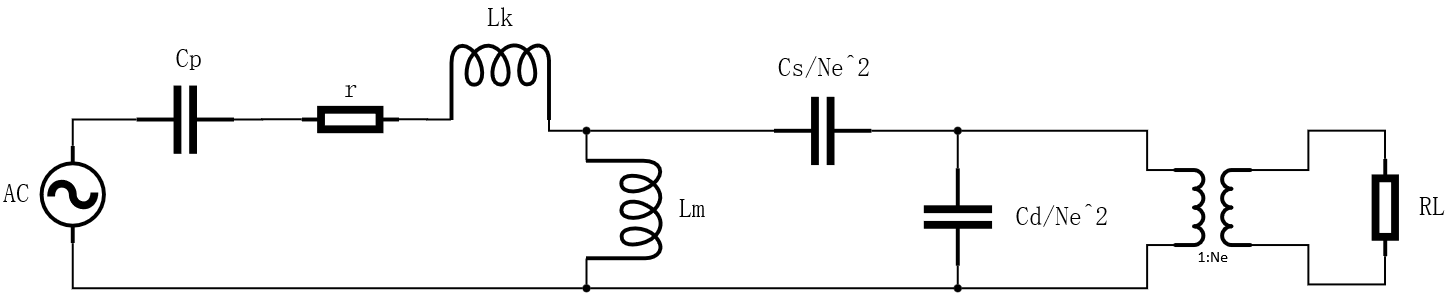
一般无线充电TX端为全桥逆变电路,输入的不是正弦波,而是方波。方波的一次谐波为$\frac{4}{\pi}Vin$;如果是半桥则是 $\frac{2}{\pi}Vin$
输出端通过全桥整流,则RL变为 $\frac{8RL}{\pi^2N_e^2}$
Cs变为: $\frac{C_s}{N_e^2}$
Cd变为: $\frac{C_d}{N_e^2}$
则整个电路的Gain为: $G=\frac{V_{rect}}{Vin}\frac{4}{\pi}$
使用实例配合仿真电路进行验证。忽略r和Cd。各元件参数为:
L11=8uH
L22=20uH
k=0.5
Cp=0.4uF
Cs=0.3uF
RL=50,100,1k
使用以上参数仿真,仿真电路如下图所示4。
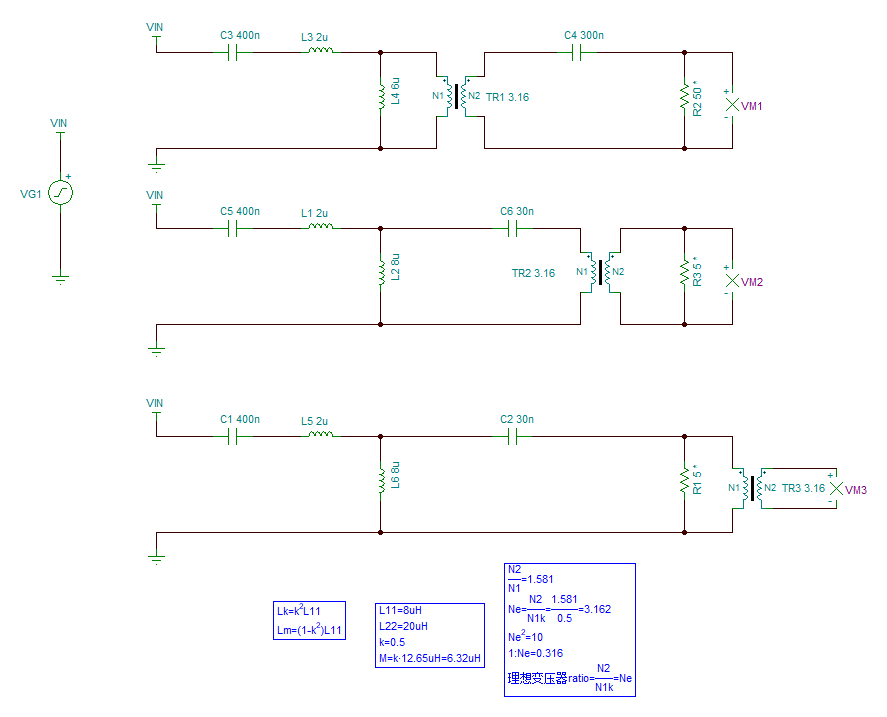
等效电路中变压器N1:N2=1:Ne。而TINA中理想变压器的ratio=V2/V1=N2/N1。故等效电路的Ne=ratio。
对RL=50,100和1K进行仿真对比。如下图所示。
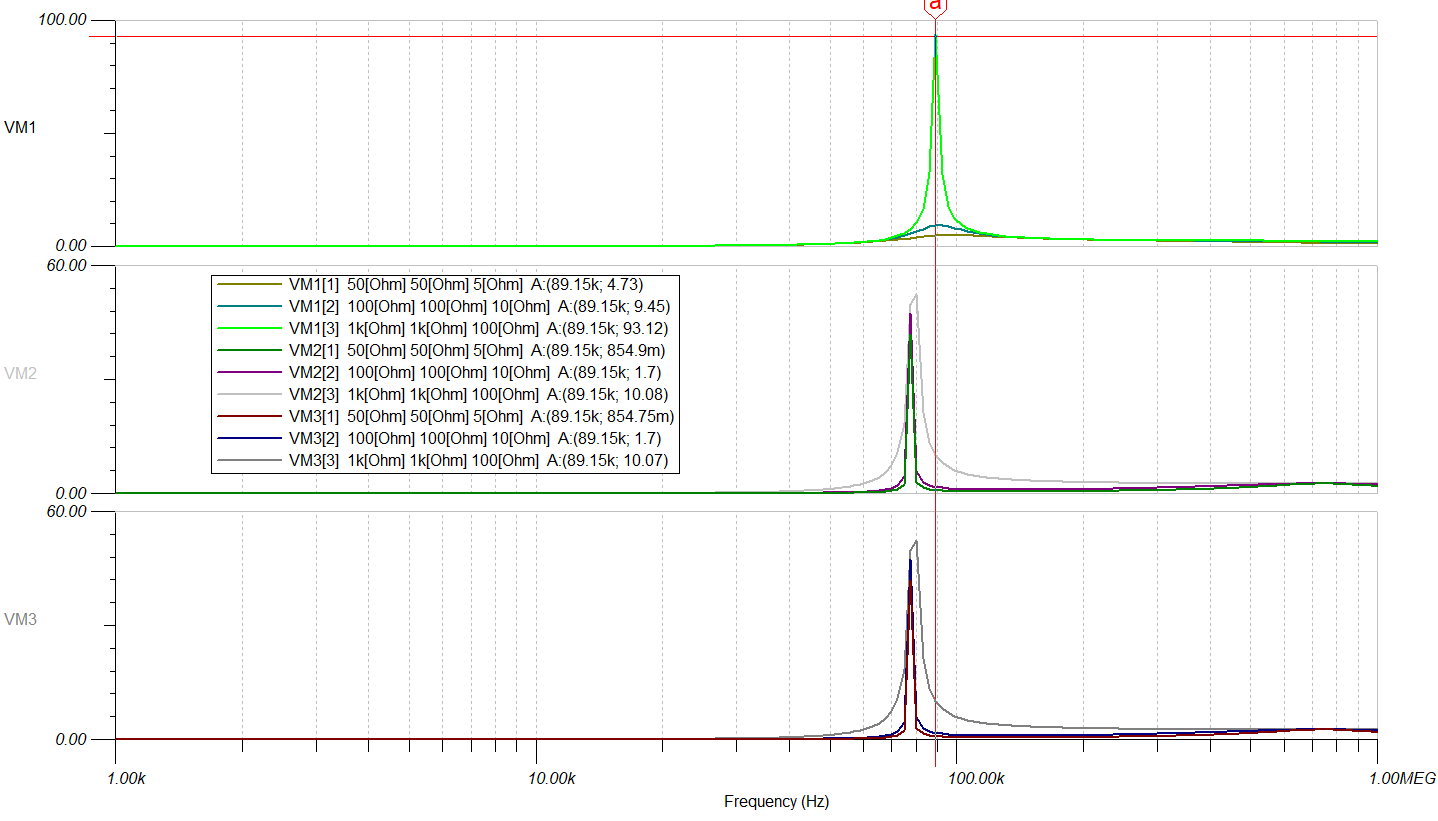
由上图可知,3个模型中后两者(VM2和VM3)一样,谐振频率发生偏移,只可作为参考分析。故后续只用模型1。
F0
谐振频率f0由Cp与Lk产生,为:$f_0=\frac{1}{2\pi\sqrt{C_pL_k}}$。
空载时谐振频率为fp,为:$f_p=\frac{1}{2\pi\sqrt{C_p(L_k+L_m)}}=\frac{1}{2\pi\sqrt{C_pL_{11}}}$。
上例子中,f0=177.94kHz,fp=88.97kHz。仿真结果如下图所示。
仿真结果与计算基本相符。
Zin
首先忽略Cd的作用,Cd=0,只考虑Cs,同时r较小,可以省略,r=0。
则Zin的传递函数为:$Zin(s)=\frac{1}{sC_p}+sL_k+sLm||({\frac{1}{sC_s'}+RL'})$,其中Cs‘和RL’为等效变换后的。将$s=jw$带入,可算出幅频函数 $Zin_(jw)$ 和相位角 $\phi(w)$ 。当 $Im(Zin)=0$ 时,计算的频率为谐振频率,此时 $|Zin(jw)|$最小。这种情况下可以计算不同负载情况下的谐振频率。
这里存在2个特殊值:RL最小时(就是短路)情况下和RL最大时(就是开路)。
RL短路时,f>f0的都是感性(满足ZVS条件)。
RL开路时,大于fp的都是感性。
其实对于大于f0(也就大于fp),Zin都是感性,与RL无关。可以通过Zin的复数看出来。
这里还存在一个RL,对于fx<f<f0,只要RL小于该RL则Zin都是感性。该值可解释为存在某一个RL=R0,对于fx<f<f0都可以使Zin的复数为0,当RL大于R0时为感性,当RL大于R0时为容性。fx~f0为感性的频率范围。
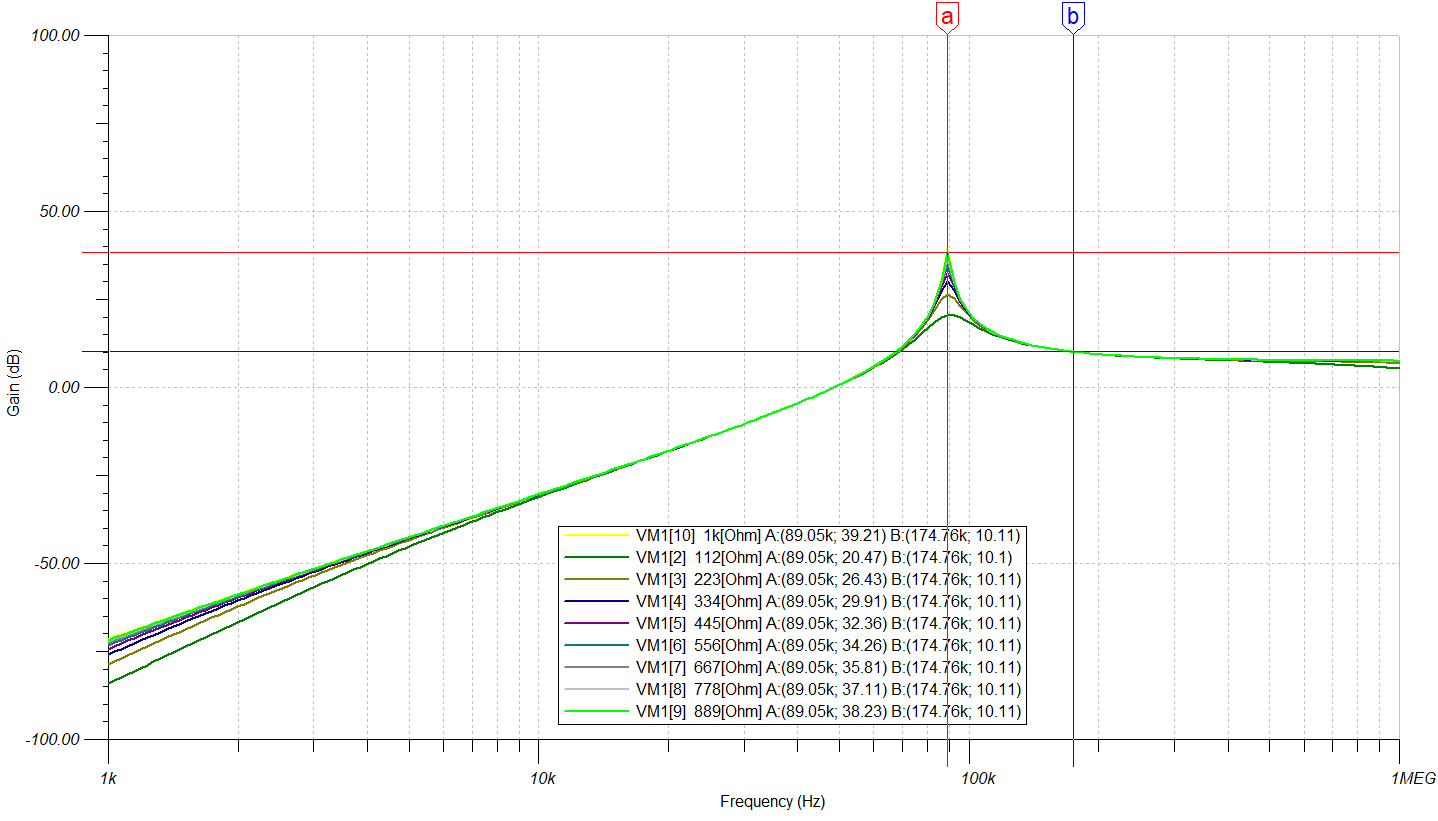
该值计算麻烦,使用仿真的方式进行推测。仿真RL=1~50Ω的结果如下图所示。
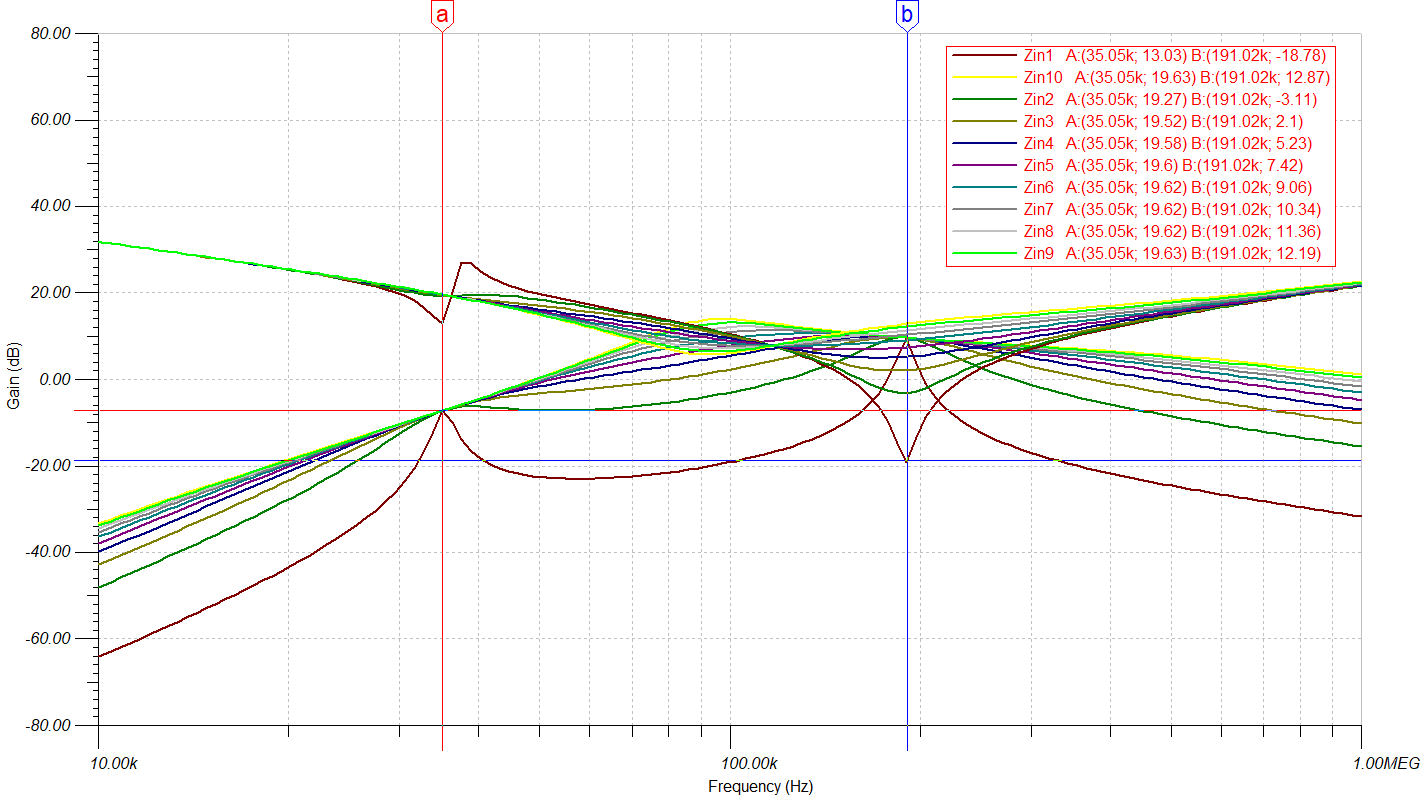
在a右边Zin也会表现出感性,此处Zin与RL有关,大约在50Ω左右,即负载小于50欧姆时系统在某范围(图中a到f0)的频率内为感性。
直接仿真
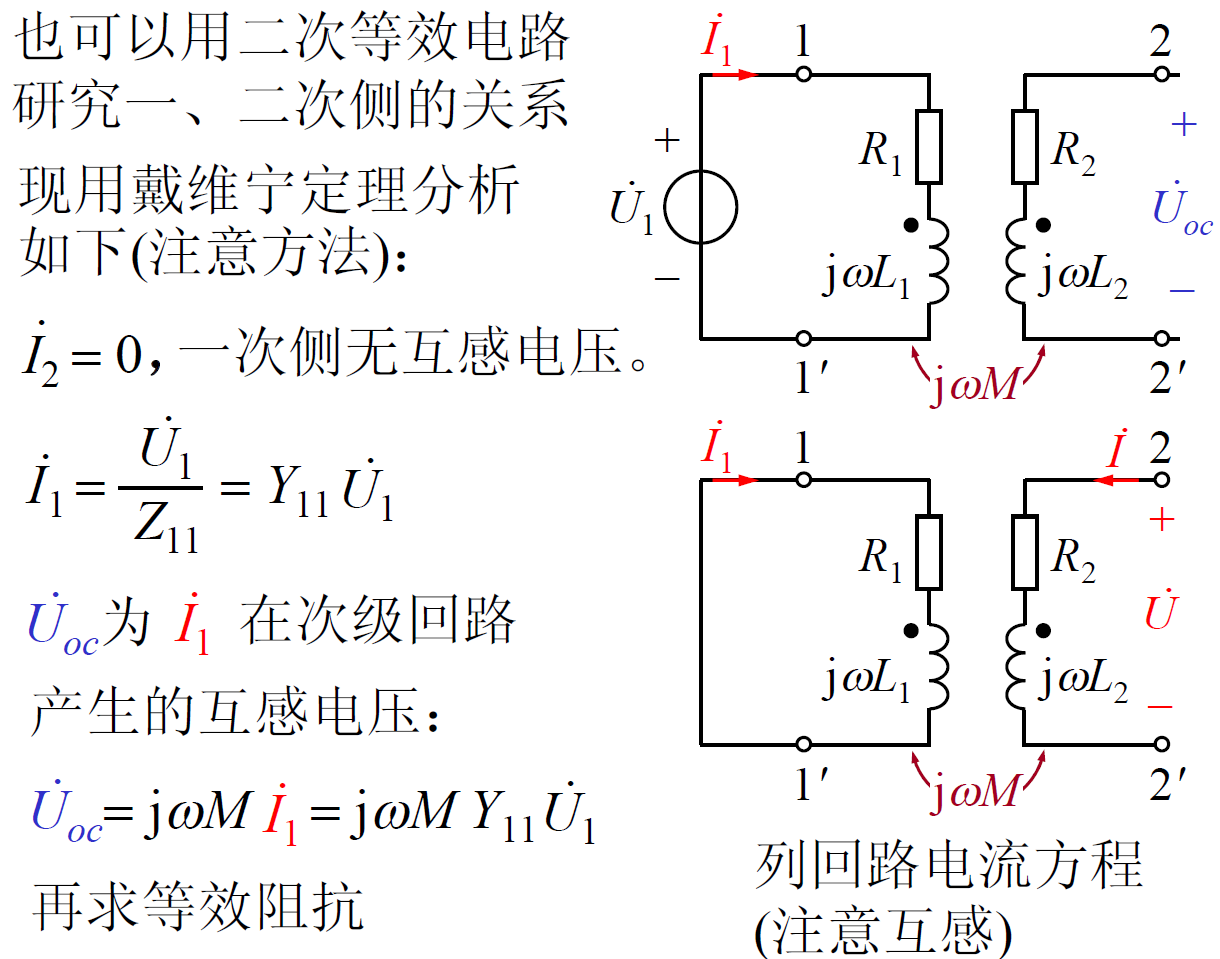
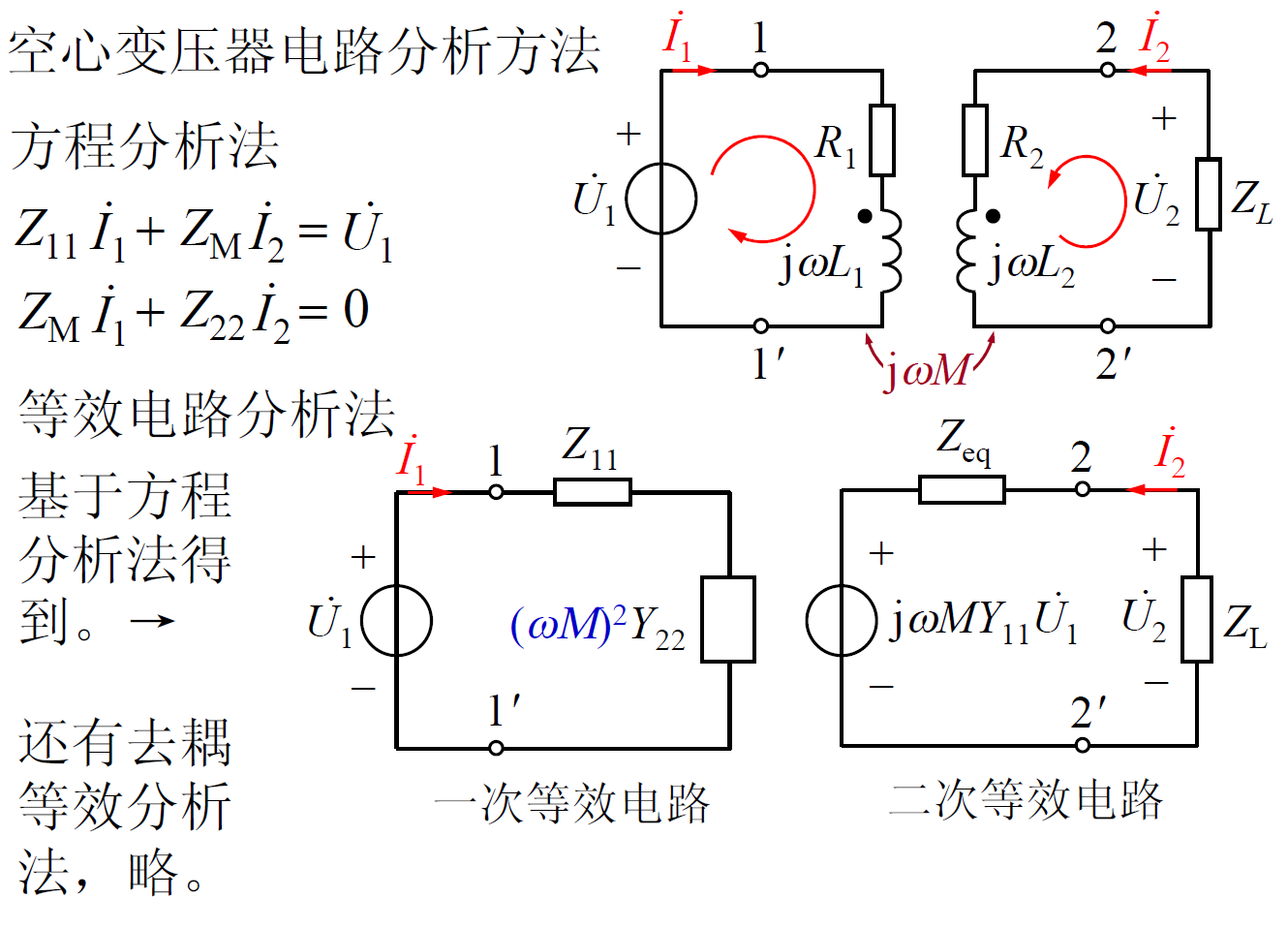
使用互感模型直接仿真。推导过程如下所示。
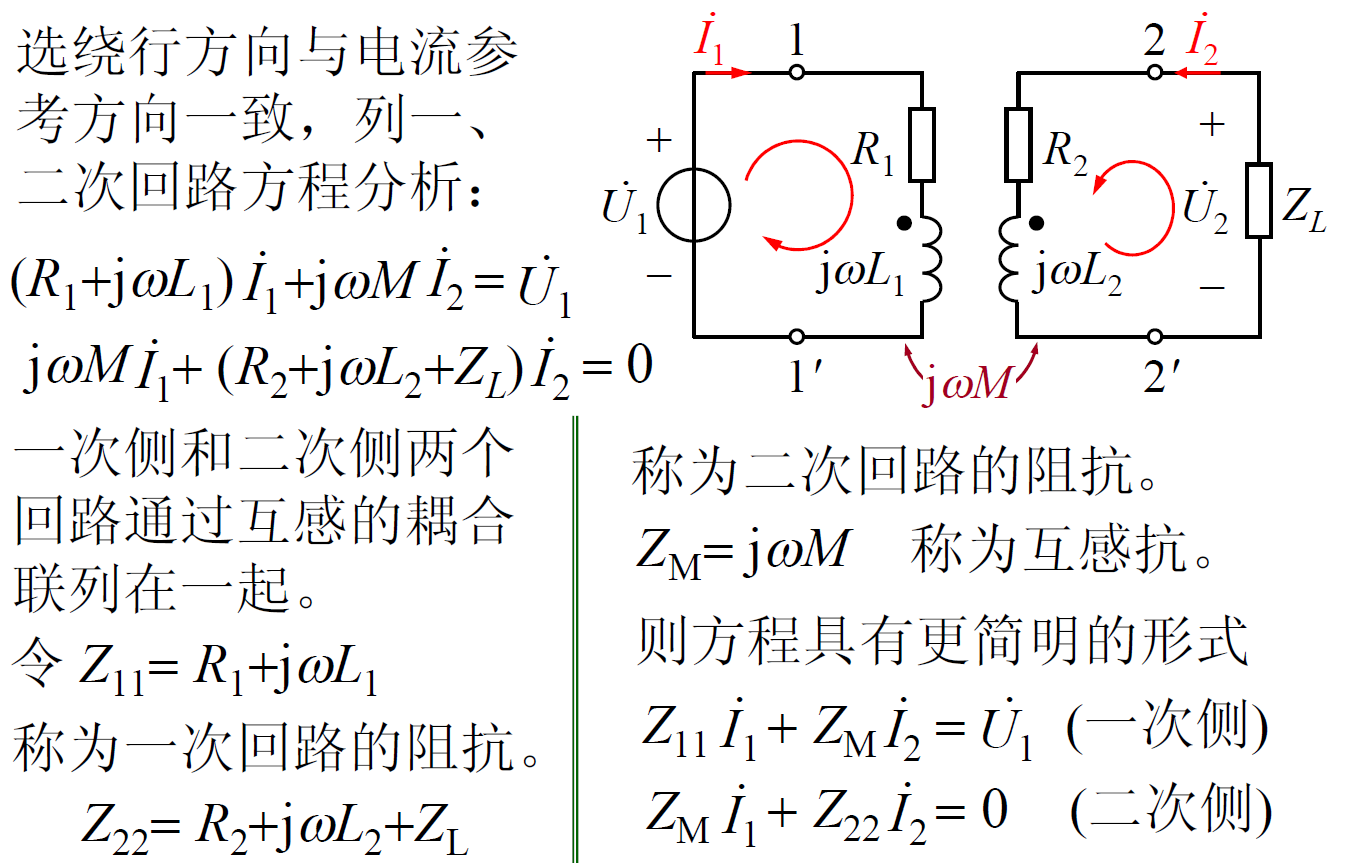
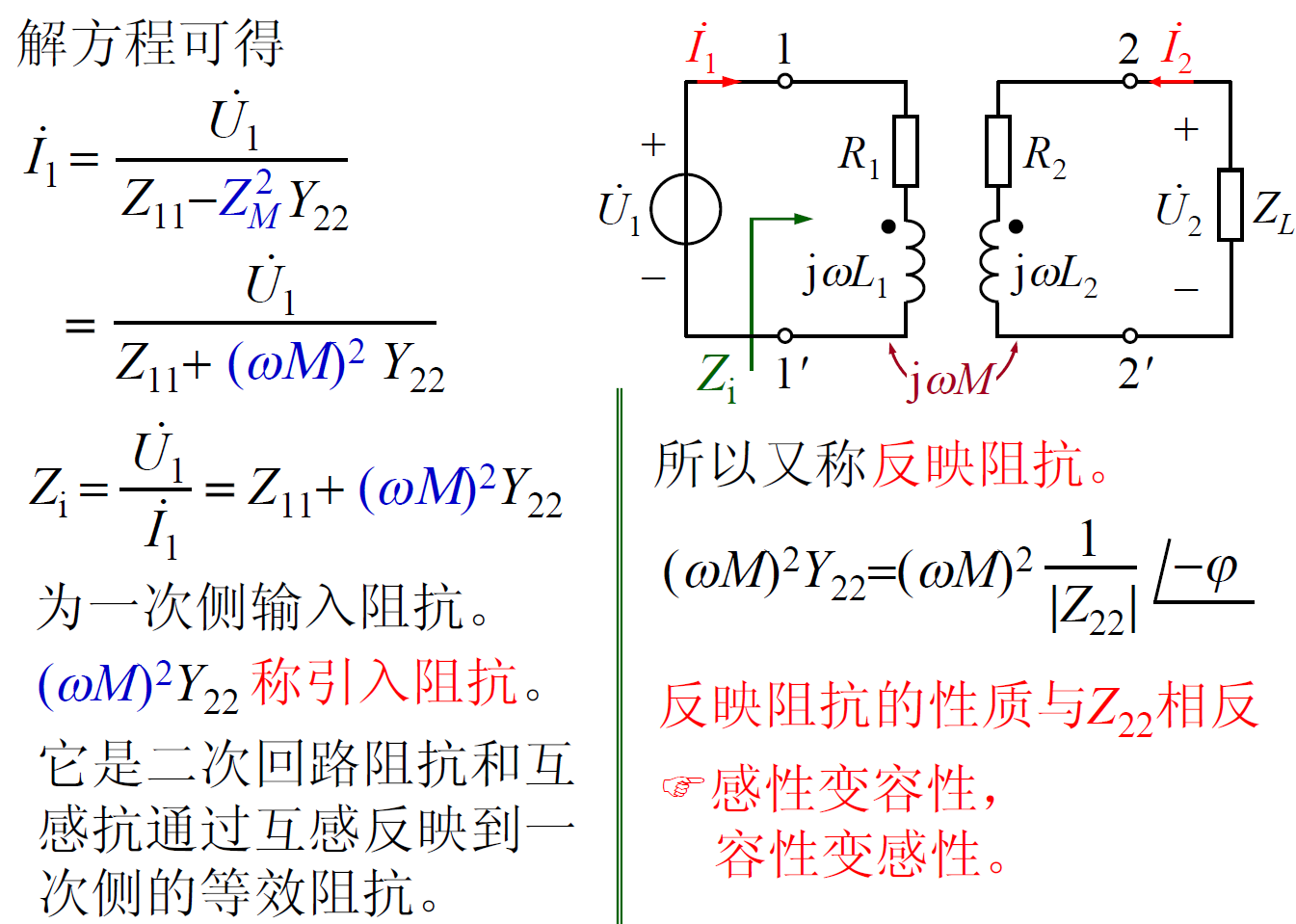
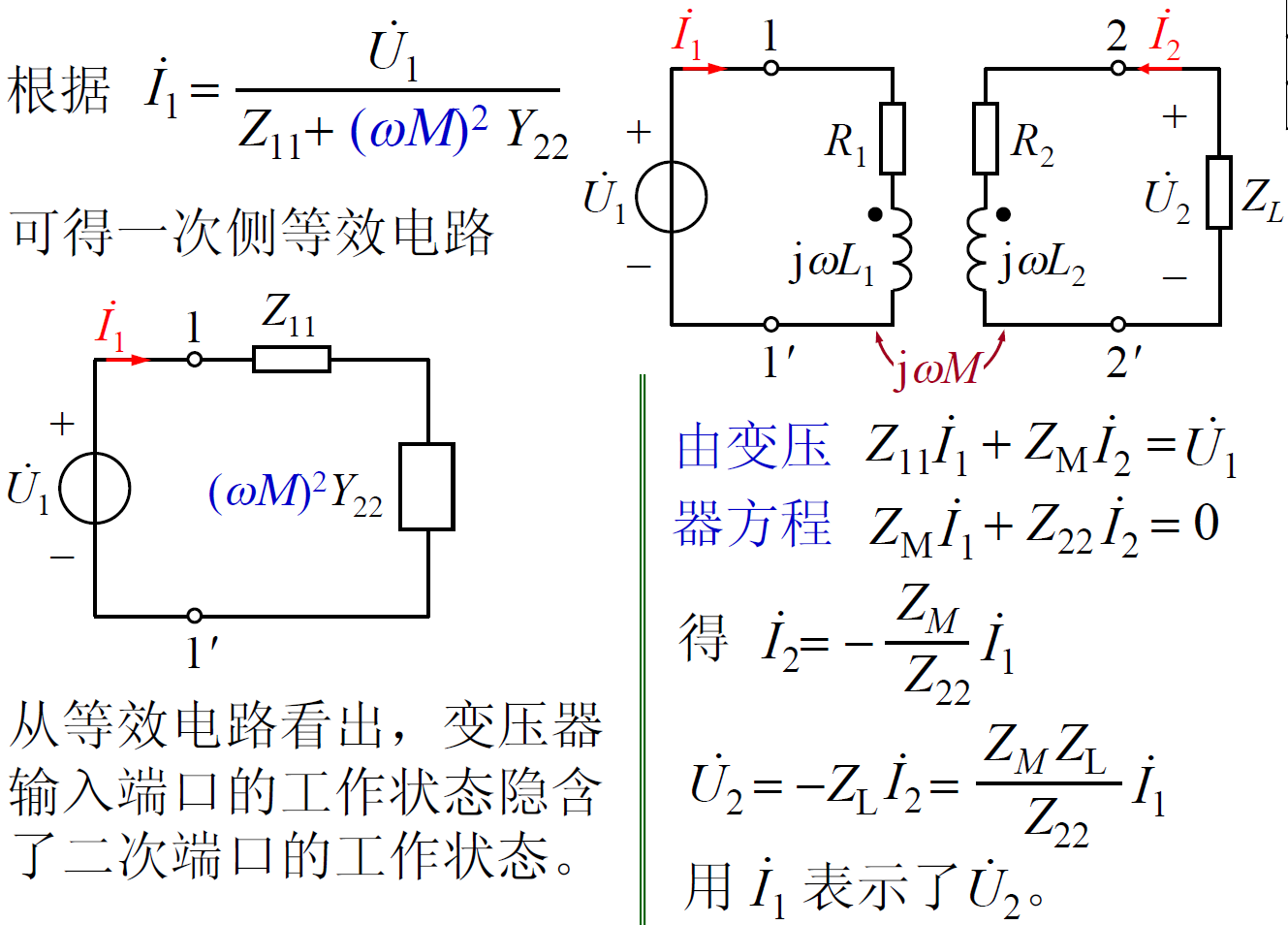

F0
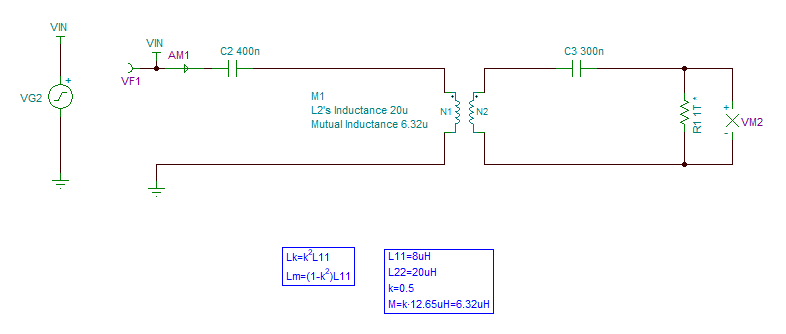
耦合模型仿真电路如下图所示。
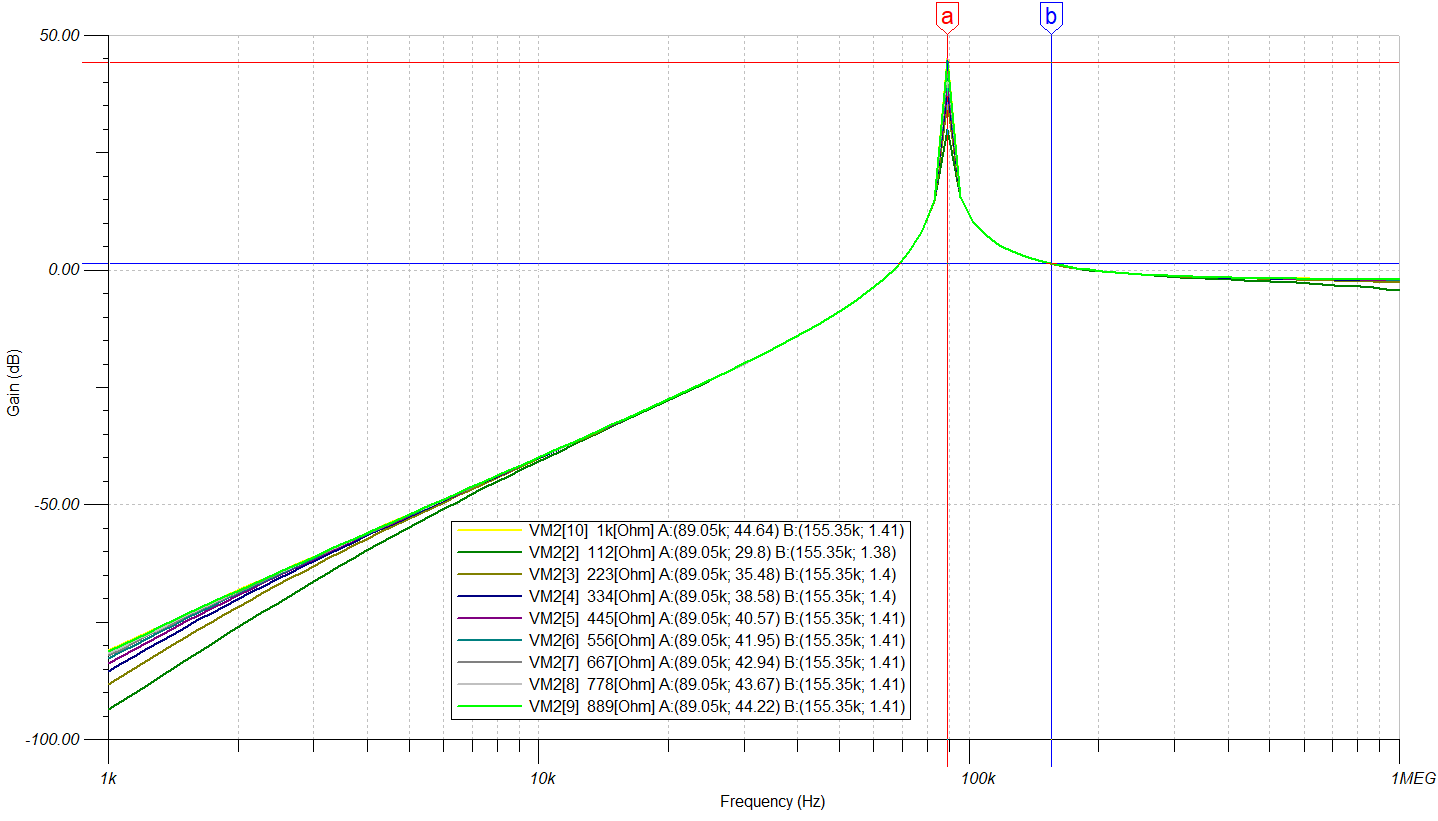
可见f0=155.35kHz,fp=89.05kHz。与等效电路模型相差不大。
Zin

这里奇怪的是,Zin的谐振点在fp处附近。推算的Zin为5Ω左右。与等效电路仿真的相差Ne^2倍。
对比两个模型,发现增益曲线不同。
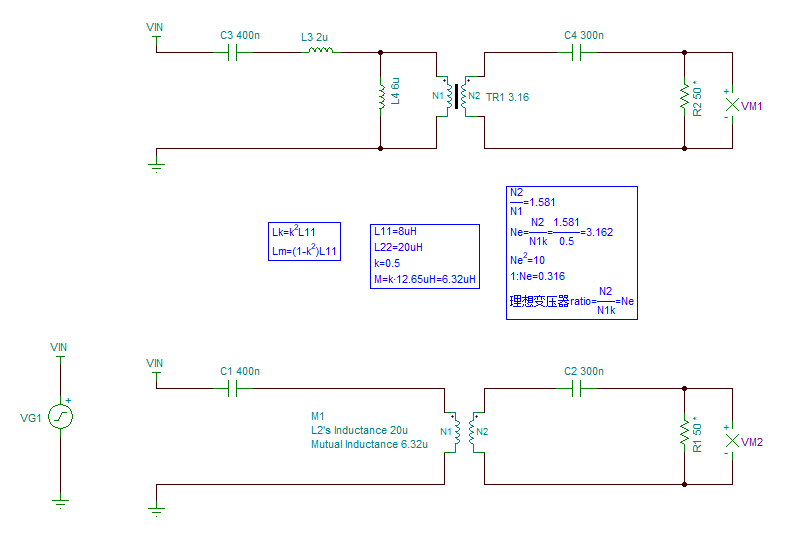
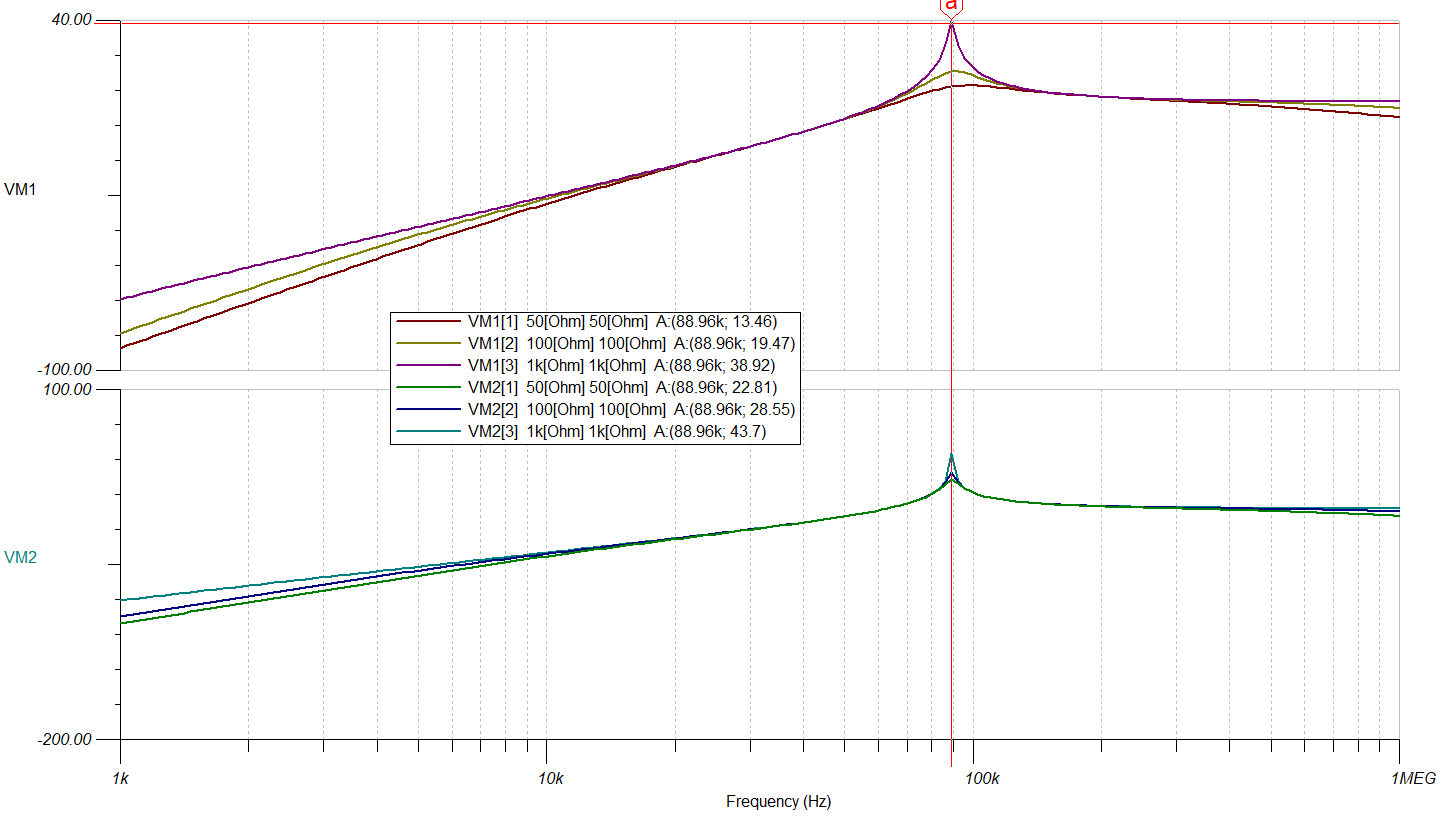
增益相差较大,但是频率相同。
虽然研究的不深入,但是网上有很多论文可以参考。后续详细参数设计参考5。
以后有机会再研究更新下。

