AI摘要:本文讨论了运算放大器(Op-Amp)的稳定性分析,特别是零极点设计对系统稳定性的影响。文章首先解释了相位裕度(PM)的重要性,指出PM应大于45°以避免振荡。接着,文章通过图解方式展示了1/β曲线(即闭环增益曲线)与Aol(开环增益)的关系,以及如何通过调整零点和极点来优化系统性能。文章还提到了TI推荐的“10倍频”方法,这是一种在高频处设置极点以提高系统带宽的策略。最后,文章通过实际例子展示了如何应用这些理论来设计稳定的Op-Amp电路。
Powered by AISummary.
运算放大器稳定性分析——零极点设计
根据相位裕度的定义,可知,Aolβ的0dB点的相位变化与180°的差就是相位裕度,此点对应的是Aol与1/β的交点(fcl)。按要求,相位裕度要大于45°,以防止其他原因(如寄生电容)导致增加零极点。如果相位裕度小于45°,出现零极点必然会出现相位变化大于180°。加入相位裕度为50°,即使出现零极点,最后也有5°的裕度,不会出现振荡。
以下图为例。

故1/β曲线只能下降到0dB。
那么1/β的最大值呢?假设1/β>Aol,则Acl≈0(趋近于0),即无法放大,信号无法到达输出端,输出端近乎为0。
有上式可知,CpRp和(Cn、Rn、RI)产生零点、CnRn和(Cp、Rp、RF)产生极点,零点处1/β曲线上翘,极点处下掰。若Rp=Rn=0,则变为(Cn、RI)产生零点,(Cp、RF)产生极点。
观察运放的开环增益曲线,在高频位置还能发现多个极点(极点导致高频增益降低)。按照TI教程 ,推荐选择开环高频处的极点作为交叉点。
相位上极点减小45°,零点增加45°;幅度上极点下摆20dB/decade,零点上摆20dB/decade。
假设极点数为P,零点数为N,则相位变化|P-N|*45°。由于相对稳定的相位裕度为45°,故|P-N|≤3。
但是如果零点于极点位置一样(比如1-s/1+s,频率一样,相位相反,这种称为“共轭复数”),则会导致1/β曲线出现“尖尖”。对于多反馈路径的系统要格外注意。
举例1如下图所示。
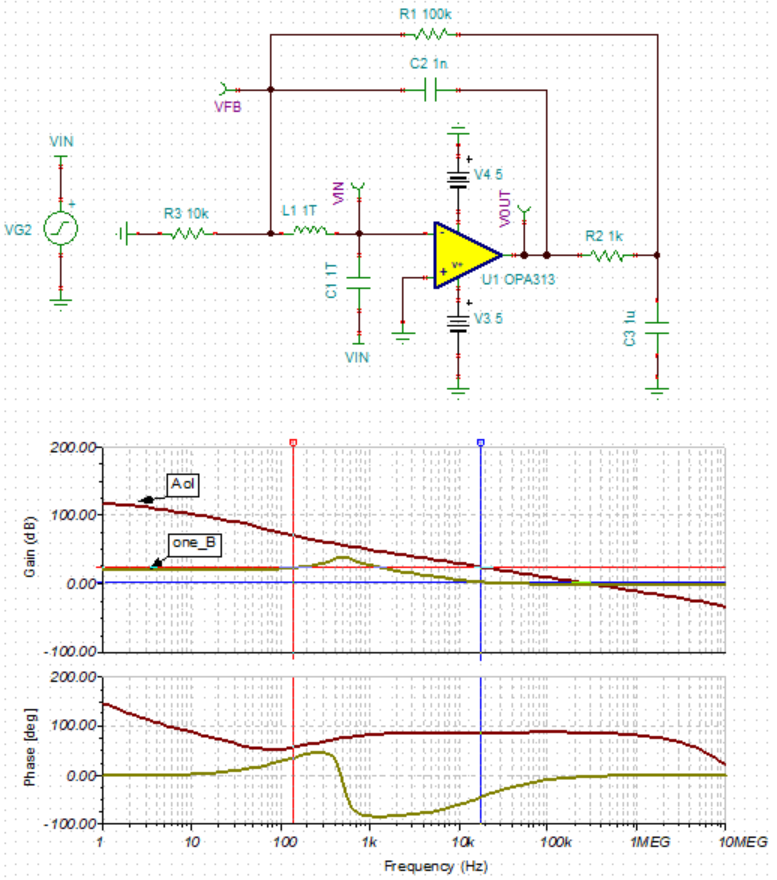
C2和R1为两个路径的反馈,C2反馈路径提供1/β的极点@160Hz,R1反馈路径提供零点@16kHz。两个路径交叉,导致出现幅度尖峰,相位出现近90°的变化。
使用脉冲信号进行仿真2,如下图所示。
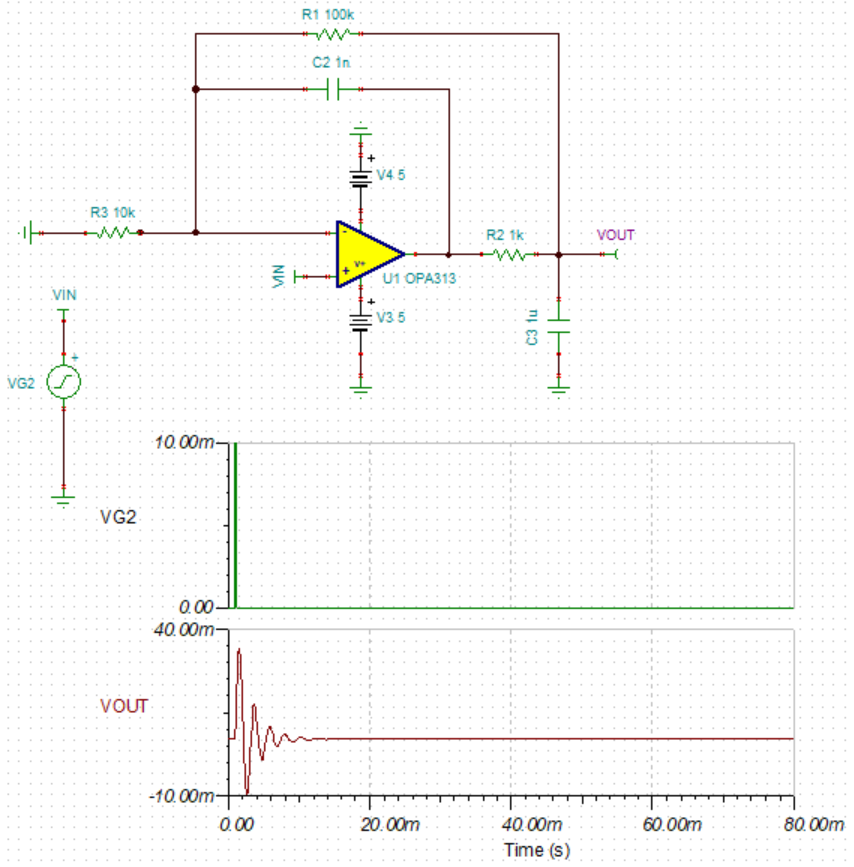
出现了极大的阻尼振荡。
TI推荐的“10倍频”方法为:
- 假设Aol的第二极点频率(通常为高频)就是闭环极点频率,这样带宽比较高。第二极点为fcl也是fp2,该地方Aolβ=1=0dB,为Aol与1/β交叉处。
- 若1/β产生的某个零点曲线上翘导致ROC为40dB/decade,则在该零点往后的10倍频处设置极点拉直,此时会与Aol交叉。
- 若交叉点频率满足设计要求,结束。
- 若不满足,需要增加拐点(极点+零点)提高带宽。可知1/β与Aol相交处小于fcl,即偏上。
- 往前fcl/10处设定零点将1/β拉直与Aol相交。
- 往前fcl/100处设定极点,将步骤2的曲线往下弯曲。这样步骤2拉直后因极点下摆,然后因零点拉平,将1/β下拉到fcl交点。
- 如果1/β为直线,不含零极点,考虑与Aol交点频率(即带宽)是否满足要求。不满足则以Aol第一极点fp1为起点,通过fp1的“10倍频”(10fp1)方式往后推导,增加零极点;或者倒过来,以fcl的“10倍频”(fcl/10)方式往前推导。
- 另外,也要注意1/β最小为0dB,即再怎么拐最终都是0dB直线。所以当fp2确实很大,导致Aol为负dB时,可选择Aol单位增益频率或者1/10倍处。
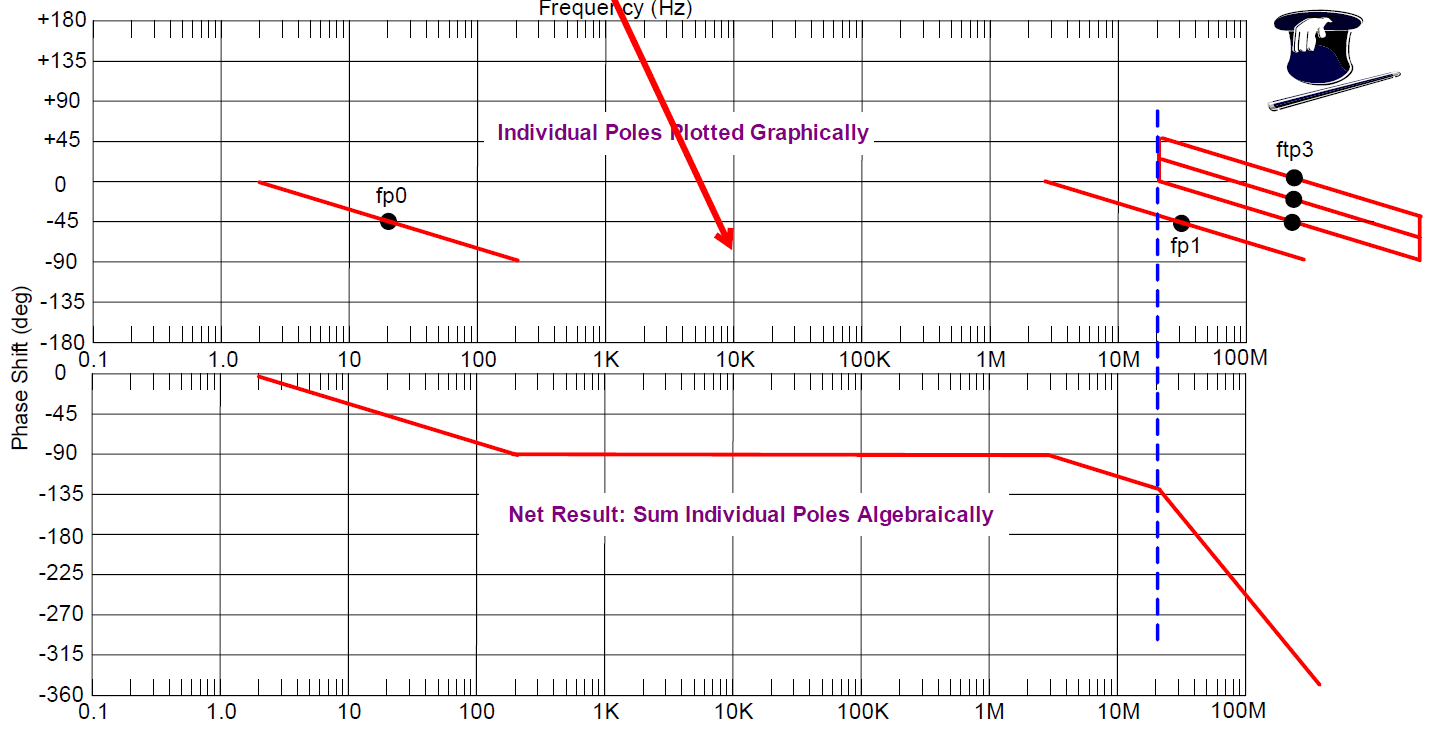
眼见为实,举例说明。如图所示。
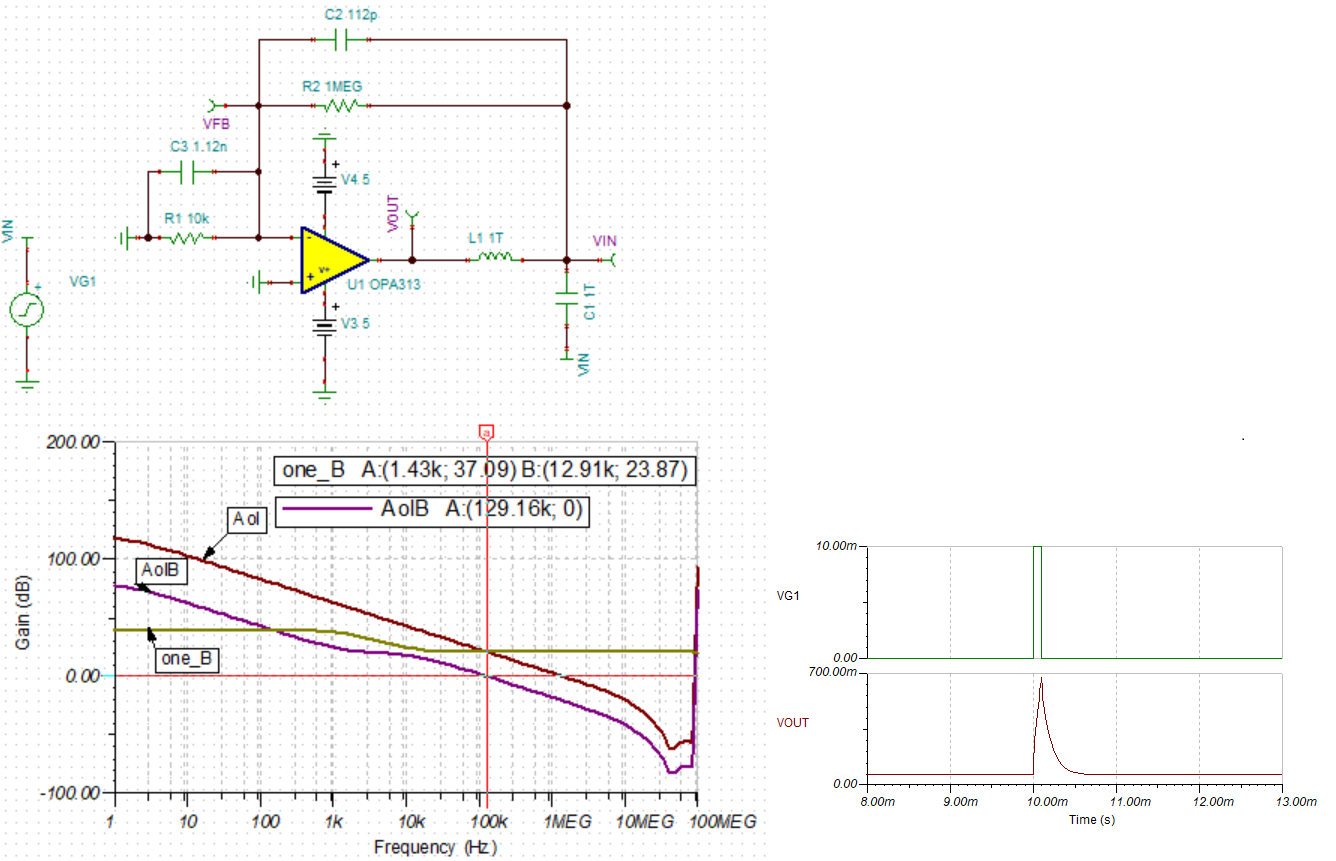
Aol为0dB时为1.42MHz,以142KHz为终点设计。则前一个零点为14.2kHz,再前一个极点为1.42kHz。与仿真结果的129.16kHz相近。脉冲响应并未出现振荡。

