AI摘要:放大器变振荡器原理探讨了运算放大器在容性负载下可能产生的不稳定性问题。文章首先解释了运算放大器的输出电阻与容性负载共同作用下,可能导致电路在特定频率下产生极点,从而影响电路的稳定性。为了解决这一问题,文章提出了三种处理容性负载的方法:噪声增益操控、环外补偿和环内补偿。这些方法通过调整电路的增益、引入额外的零点和极点,以及改变反馈环路的配置,来提高电路的稳定性。文章还强调了在设计过程中,应确保负载电容为已知且恒定的值,以便更准确地应用这些补偿技术。
Powered by AISummary.
放大器变振荡器原理
运算放大器固有的输出电阻Ro与容性负载一起,构成放大器传递函数的另一个极点。如波特图所示,在每个极点处,幅度斜率(负值)减小20dB/10倍。请注意各极点如何增加多达-90°的相移。我们可以从两个角度来考察不稳定性问题。请看对数图上的幅度响应,当开环增益与反馈衰减之和大于1时,电路就会变得不稳定。类似地,还可以看相位响应,在环路相移超过-180°的频率,如果此频率低于闭环带宽,则运算放大器往往会发生振荡。电压反馈型运算放大器电路的闭环带宽等于运算放太器的增益带宽积(GBP,或单位增益频率)除以电路的闭环增益(ACL)。
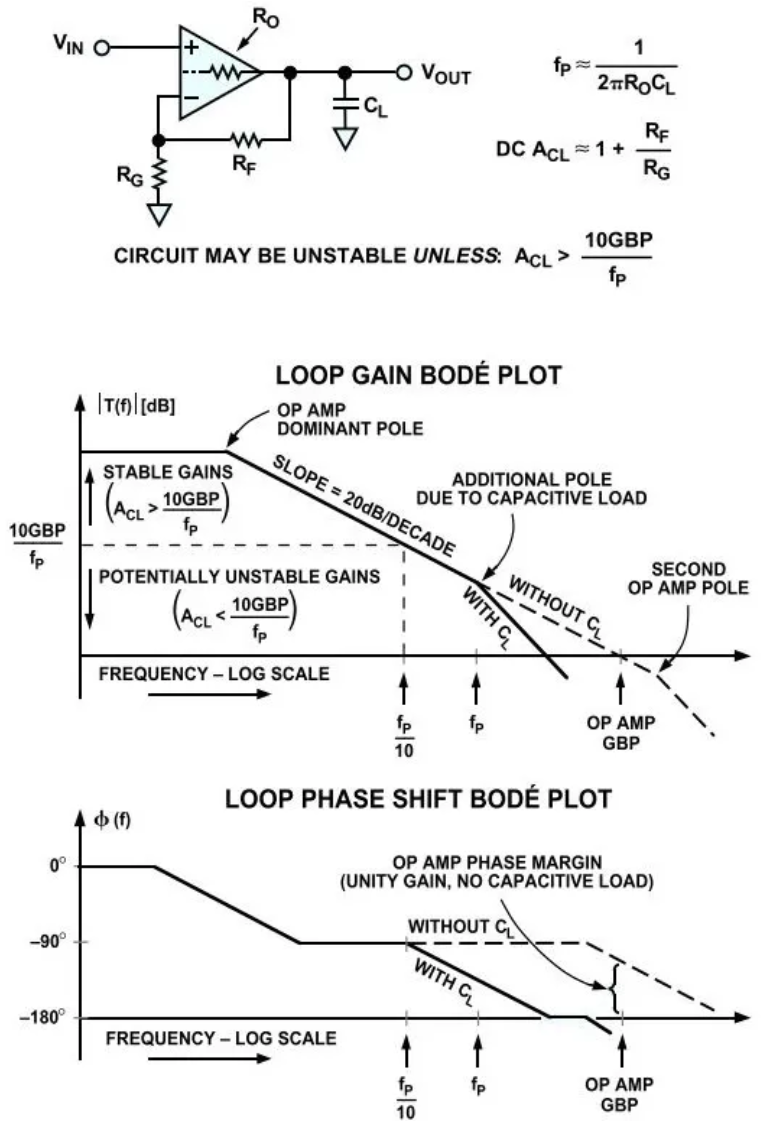
运算放大器电路的相位余量可以看作是使电路变得不稳定时所需的闭环带宽的额外相移量(即相移+相位余量=-180°)。随着相位余量趋于0,环路相移趋于-180°,运算放大器电路便趋于不稳定。通常而言,如果相位余量值远小于45°,就会导致频率响应的尖峰,以及阶跃响应时的过冲或响铃振荡等问题。为了保持足够的相位余量,容性负载所产生的极点至少应比电路的闭环带宽高10倍。如果不是这样,请考虑电路不稳定的可能性。
如何处理容性负载?教你三招
首先应当确定,运算放大器能否安全地驱动自身负载。许多运算放大器数据手册规定了“容性负载驱动能力”,另有一些则提供了关于“小信号过冲与容性负载之间关系”的典型数据。查看这些数值,可以发现过冲随着负载电容增加成倍递增。当过冲接近100%时,运算放大器便趋于不稳定。如果可能,请让过冲远低于此限值。另外请注意,此图针对特定增益而言。对于电压反馈型运算放大器,容性负载驱动能力随着增益的增加而提高。因此,在单位增益时能够安全驱动100pF电容的电压反馈型运算放大器,在增益为10时应当能够驱动1000pF电容。
一些运算放大器数据手册给出了开环输出电阻(Ro),由此可算出上述附加极点的频率。如果附加极点的频率(fp)比电路带宽高出10倍,电路将保持稳定。
如果运算放大器的数据手册没有说明容性负载驱动能力或开环输出电阻,并且没有提供过冲与容性负载的关系图,那么为了确保稳定性,必须假设任何负载电容均要求采取某种补偿技术。有许多方法都能使标准运算放大器电路稳定驱动容性负载,下面是其中几种:
噪声增益操控
这是一种在低频应用中保持稳定的有效方法,然而却经常被设计人员所忽略。其原理是提高电路的闭环增益(也称为“噪声增益”),而不改变信号增益,从而降低开环增益与反馈衰减之积变为1的频率。在一些电路的运算放大器输入端之间连接RD即可实现,如下图所示。利用所给的公式可求得这些电路的“噪声增益”。
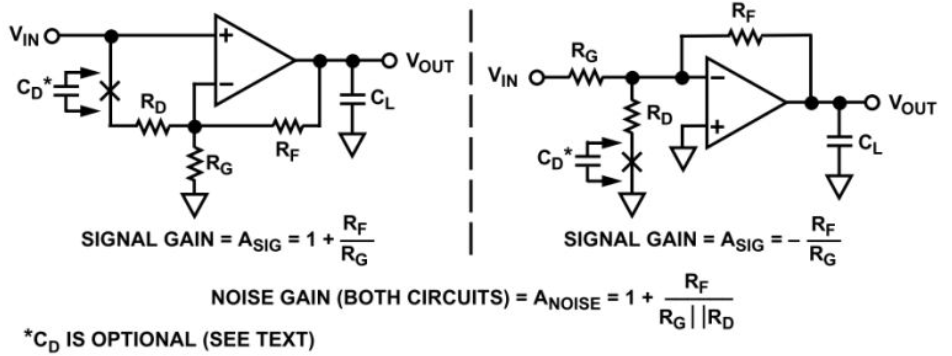
由于稳定性受噪声增益而不是信号增益控制,因此上面的电路可提高稳定性,且不会影响信号增益。只需使“噪声带宽”(GBP/ANOISE)比负载所产生的极点至少低10倍,便可确保稳定。
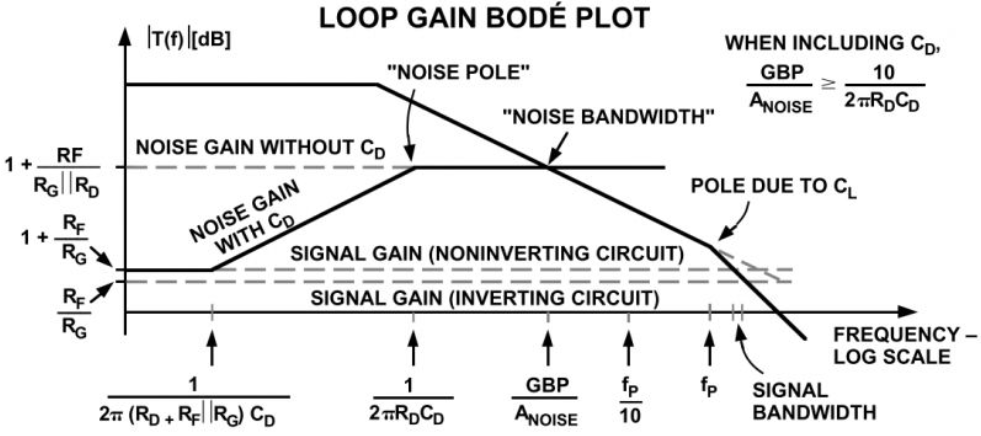
这种稳定方法有一个缺点,即折合到输入端的电压噪声和输人失调电压进一步放大,导致输出噪声和失调电压增加。将电容CD与RD串联,可以消除增加的直流偏置电压,但这种技术会增加噪声,无法消除。这些电路在包含CD和不含CD两种情况下的有效噪声增益如图所示。
使用时,CD应尽可能大;最小值应为10ANOISE/(2πRDGBP),才能使“噪声极点”至少比“噪声带宽”低10倍。
环外补偿
这种方法是在运算放大器的输出端与负载电容之间增加一个电阻RX,如下图所示。该电阻显然在反馈环路之外,但它与负载电容一起,可将一个零点引人反馈网络的此传递函数,从而减小高频时的环路相移。
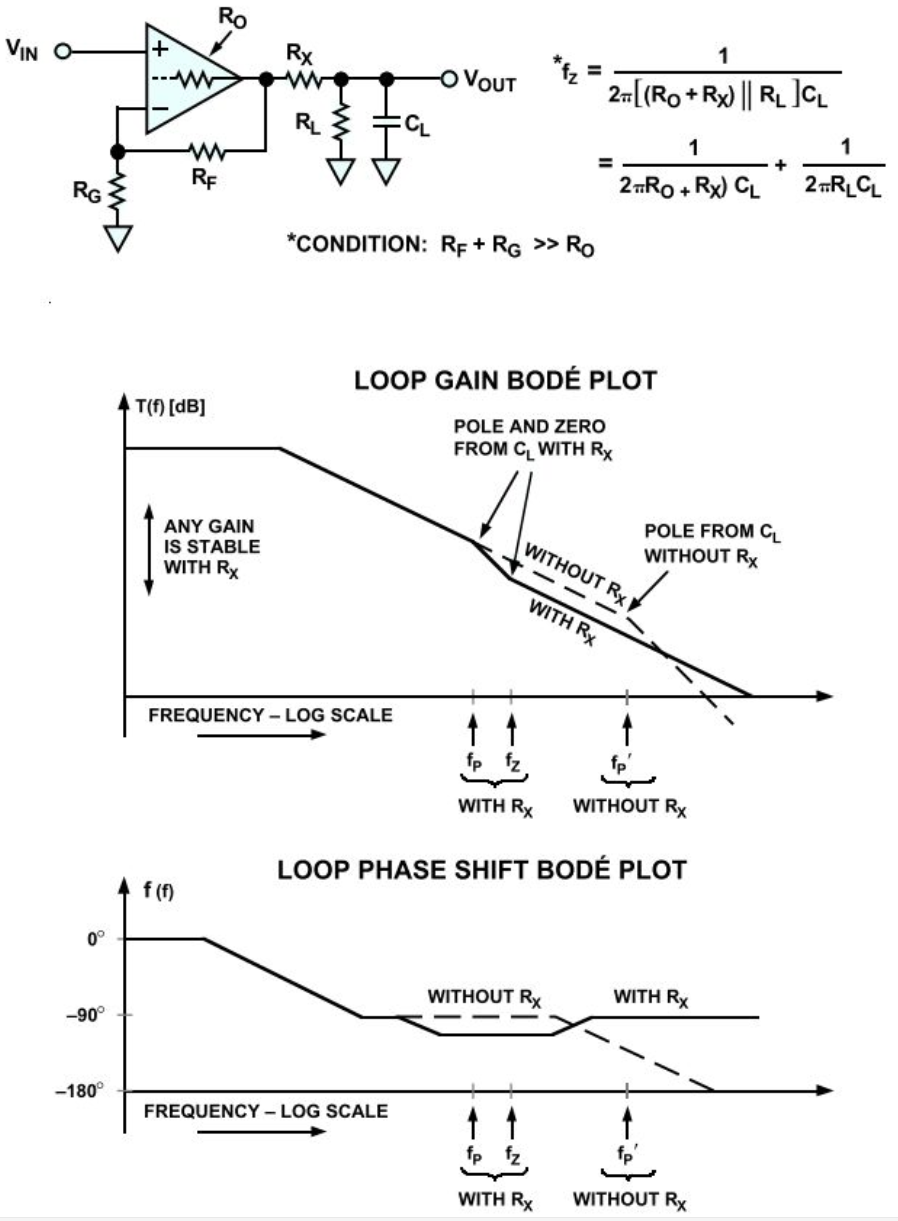
为确保稳定,RX值应使所增加的零点(fZ)至少比运算放大器电路的闭环带宽低10倍。增加RX后,电路性能不会像第一种方法一样受到影响,输出噪声不会增加,但相对负载而言的输出阻抗会提高。由于RX和RL构成电阻分压器,这可能会降低信号增益。如果RL已知且相当稳定,则可以提高运算放大器电路的增益,以抵消该增益损失。
这种方法对于驱动传输线路非常有效。为了避免驻波,RL和RX的值必须等于电缆的特性阻抗(一般为50Ω或75Ω)。因此,RX是预先确定的,剩下的工作就是让放大器的增益加倍,以便抵消电阻分压器造成的信号损耗,这样问题就解决了。
环内补偿
如果RL是未知的或动态变化的,则增益级的有效输出电阻必须保持较低。这种情况下,将RX连接在整个反馈环路以内可能有帮助,如下图所示。采用这种配置,直流和低频反做来自负载本身,因此从输入端到负载的信号增益仍然不受分压器(RX和RL)的影响。
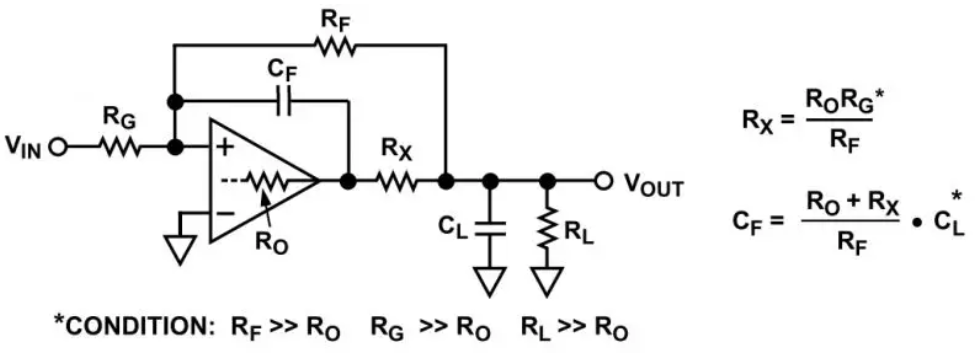
此电路中增加的电容CF可以抵消CL所造成的极点和零点。简单地说,CF所产生的零点与CL所产生的极点一致,同时CF所产生的极点与CL所产生的零点一致。因此,总传递函数和相位响应与没有电容时完全一样。为了确保极点和零点组合均得以抵消,必须精确求解上述方程式。另外应注意条件;如果负载阻抗相对较大,则这些条件很容易得到满足。
如果RO未知,将难以计算。这种情况下,设计程序就变成猜谜游戏,这可以说是电路设计的噩梦。关于SPICE,有一点应当注意:运算放大器的SPICE模型并未精确模拟开环输出电阻(RO),因此并不能完全取代补偿网络的经验设计。
还有一点必须注意:CL必须为已知且恒定的值,才能应用这种技术。许多应用中,放大器驱动非常规负载,CL可能会因负载不同而有很大差别。只有CL是闭环系统的一部分时,使用以上电路才是最佳选择。
一种应用是对基准电压进行缓冲或反相,以驱动较大的去耦电容。此时,CL为固定值,可以精确抵消极点/零点组合。这种方法的低直流输出阻抗和低噪声(与前两种方法相比)非常有利。此外,基准电压的去耦电容可能很大(经常为若干微法),使用其它补偿方法并不可行。
以上三种方法均应用于“标准”、单位增益稳定、电压反馈型运算放大器,每种方法各有利弊。现在,您可以应用自己的知识来判断哪种方法最适合您的应用啦~

