AI摘要:本文详细分析了圆形活塞声场的声压分布,包括远场和近场的情况。在远场,通过近似计算得到了声压的表达式,并引入了贝塞尔函数。在近场,分析了中心轴上的声场,得到了声压的表达式,并讨论了临界距离的概念。文章还提供了指向性的计算代码和图表,帮助理解声场的指向性特性。
Powered by AISummary.
超声——圆形活塞声场
圆形活塞如下图所示。
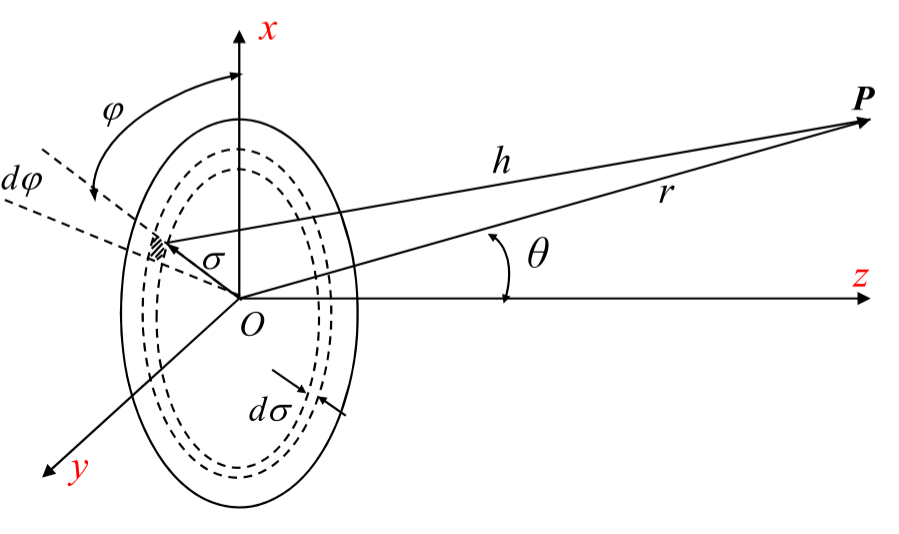
将每个小面元看做点声源,其在p点的声压就是整个圆面的点声源声压的积分。根据之前的球面声场:假设Q为声源强度(体积速度)为:$Q=u_a S$,可知小面元的声源强度为:$dQ_0=u_adS$。
对于图中声源到观测点的距离为h,故半空间点声源的声压为:$p=j\frac{\rho_0C_0kQ}{2\pi h}e^{j(wt-kh)}$,对于小面元则为:$dp=j\frac{\rho_0C_0k}{2\pi h}dQ_0e^{j(wt-kh)}$。
P点为观察点,位于xoz平面内。
远场
对于远场,由于r>>a,a就是图中的$\sigma $。可推导出h的近似值。
根据三维空间向量计算公式,x、y、z轴的单位向量为:$\overrightarrow{i} ,\overrightarrow{j},\overrightarrow{k}$,则可得:
$\overrightarrow{r} =|r|(cos\theta \overrightarrow{k}+sin\theta \overrightarrow{i})$
$\overrightarrow{\sigma } =|\sigma |(cos\varphi \overrightarrow{i}+sin\varphi \overrightarrow{j})$
$\overrightarrow{r} \times \overrightarrow{\sigma }=|r|(cos\theta \overrightarrow{k}+sin\theta \overrightarrow{i})\times |\sigma |(cos\varphi \overrightarrow{i}+sin\varphi \overrightarrow{j})=|r||\sigma| (sin\theta cos\varphi )$
则h为:$\overrightarrow{h} =\overrightarrow{r} -\overrightarrow{\sigma } $
$|h|=\sqrt{r^2+\sigma^2-2\overrightarrow{r} \times \overrightarrow{\sigma }}=\sqrt{r^2+\sigma^2-2|r||\sigma| (sin\theta cos\varphi )}=r\sqrt{1+\frac{\sigma^2}{r^2}-\frac{2 \sigma}{r}sin\theta cos\varphi}$
由于r>>a(或者σ),故$\frac{\sigma^2}{r^2} \approx 0$,所以:
$|h|=r\sqrt{1-\frac{2 \sigma}{r}sin\theta cos\varphi}$
对后式子进行泰勒展开,比如$(1+x)^n=1+nx+...$,当|x|<<1时可以忽略二阶项,故上式为:
$|h|=r(1-\frac{1}{2}\frac{2 \sigma}{r}sin\theta cos\varphi)=r-\sigma sin\theta cos\varphi$
对dp进行积分可得p点的声压为:
$p=j\frac{\rho_0C_0k}{2\pi h}\int dQ_0e^{j(wt-kh)}=j\frac{\rho_0C_0k}{2\pi h} \int u_a dS e^{j(wt-kh)}=j\frac{\rho_0C_0k}{2\pi h} u_a e^{j(wt-kh)} \int dS $
其中在远场$h\approx r$,故分母的h可以换成r,但是e的不能直接换。则为:
$p=j\frac{\rho_0C_0k}{2\pi r} u_a e^{j(wt-kh)} \int dS =j\frac{\rho_0C_0k}{2\pi r} u_a e^{j(wt-kr+k\sigma sin\theta cos\varphi)} \int dS=j\frac{\rho_0C_0k}{2\pi r} u_a e^{j(wt-kr)} \int e^{k\sigma sin\theta cos\varphi}dS$
环形圆弧的周长为:$\int dl=\int \sigma d \varphi$
环形圆弧的面积微分为:$dS=d\sigma \int dl=d\sigma \int\sigma d\varphi$
则p为:
$p=j\frac{\rho_0C_0k}{2\pi r} u_a e^{j(wt-kr)} \int e^{jk\sigma sin\theta cos\varphi}dS=j\frac{\rho_0C_0k}{2\pi r} u_a e^{j(wt-kr)} \int e^{jk\sigma sin\theta cos\varphi}d\sigma \int\sigma d\varphi$
最终为:
$p=j\frac{\rho_0C_0k}{2\pi r} u_a e^{j(wt-kr)} \int \sigma d\sigma \int e^{jk\sigma sin\theta cos\varphi}d\varphi$,其中σ的积分范围为0~a,φ的范围为0~2π。
根据贝塞尔函数可知:
$J_0(x)=\frac{1}{2 \pi} \int_{0}^{2 \pi} e^{jxcos \varphi}d \varphi $
$\int x J_0(x)dx=xJ_1(x)$
则上式中$\int e^{jk\sigma sin\theta cos\varphi}d\varphi$改为贝塞尔函数,其中$x=k\sigma sin \theta$,代入为:
$J_0(k \sigma sin \theta)=\frac{1}{2 \pi} \int_{0}^{2 \pi} e^{jk \sigma sin \theta cos \varphi}d \varphi$
则 $dx=k\sin\theta d\sigma$ ,$\sigma=\frac{x}{k\sin\theta}$
当 $\sigma = 0$时,$u = 0$ ;当 $\sigma = a$ 时,$u = ka\sin\theta$,则
$2\pi\int_{0}^{a}\sigma J_0(k\sigma\sin\theta)d\sigma=2\pi\int_{0}^{ka\sin\theta}\frac{x}{k\sin\theta}J_0(x)\frac{dx}{k\sin\theta}=\frac{2\pi}{k^{2}\sin^{2}\theta}\int_{0}^{ka\sin\theta}xJ_0(x)dx$
由 $\int xJ_0(x)dx = xJ_1(x)$ 可得:
$\frac{2\pi}{k^{2}\sin^{2}\theta}\int_{0}^{ka\sin\theta}xJ_0(x)dx=\frac{2\pi}{k^{2}\sin^{2}\theta}\left[xJ_1(x)\right]_0^{ka\sin\theta}=\frac{2\pi}{k^{2}\sin^{2}\theta}\times ka\sin\theta J_1(ka\sin\theta)=\frac{2\pi a}{k\sin\theta}J_1(ka\sin\theta)$
于是声压变为:
$p=j\frac{\rho_0C_0k}{2\pi r} u_a e^{j(wt-kr)} \int \sigma d\sigma \int e^{jk\sigma sin\theta cos\varphi}d\varphi=j\frac{\rho_0C_0k}{2\pi r} u_a e^{j(wt-kr)}\frac{2\pi a}{k\sin\theta}J_1(ka\sin\theta)$
$p= j\frac{\rho_0C_0ka^2}{2 r} u_a e^{j(wt-kr)}\frac{2J_1(ka\sin\theta)}{ka\sin\theta}$
其中,$k=\frac{2\pi}{\lambda},c=\lambda f,w=2\pi f$,推导出$ck=2\pi f=w$,代入上式为:
$p= j\frac{\rho_0wa^2}{2 r} u_a e^{j(wt-kr)}\frac{2J_1(ka\sin\theta)}{ka\sin\theta}=jw\frac{\rho_0u_aa^2}{2 r} [\frac{2J_1(ka\sin\theta)}{ka\sin\theta}]e^{j(wt-kr)}$
对于圆面活塞,面积为$S=\pi a^2$,则$Q=u_a S=u_a \pi a^2$,代入上式则为:
$p=jw\frac{\rho_0Q}{2 \pi r} [\frac{2J_1(ka\sin\theta)}{ka\sin\theta}]e^{j(wt-kr)}$
径向速度为:
$v_r=-\frac{1}{jw\rho_0}\frac{\partial p}{\partial r}$
其中p对r的偏导为:$\frac{\partial p}{\partial r}=\frac{\partial A \frac{e^{j(wt-kr)}}{r}}{\partial r}$,A表示其他不与r相关的式子。求得:
$\frac{\partial p}{\partial r}=Ae^{jwt}\frac{\partial \frac{e^{-jkr}}{r}}{\partial r}=Ae^{jwt}[-jke^{-jkr}\frac{1}{r}+e^{-jkr}\frac{-1}{r^2}=-A\frac{e^{j(wt-kr)}}{r}[jk+\frac{1}{r}]=-p[jk+\frac{1}{r}]$
$v_r=-\frac{1}{jw\rho_0}-p[jk+\frac{1}{r}]=-\frac{1}{jC_0k\rho_0}-p[jk+\frac{1}{r}]=\frac{1}{C_0\rho_0}[1+\frac{1}{jkr}]p$
法向声强为:
$I=\frac{1}{T}\int_0^{T}Re_p Re_{v_r}dt=\frac{1}{8}\rho_0c_0u_a^2(ka)^2\frac{a^2}{r^2}[\frac{2J_1(kasin\theta)}{kasin\theta}]^2$
指向性
定义为:保持场点与声源的距离不变,任意$\theta$方向的场点声压幅值与这个距离上最大声压幅值之比。
$D(\theta)=\frac{P_a(\theta)}{P_a(\theta)|_{\theta=0}}$
θ=0时,$\frac{J_1(0)}{0}=\frac{1}{2}$,则上式为:
$D(\theta)=|\frac{\frac{2J_1(ka\sin\theta)}{ka\sin\theta}}{1}|=|\frac{2J_1(ka\sin\theta)}{ka\sin\theta}|$
当ka<1时,x趋近于0,D(θ)趋近于1,则$p=\frac{jw\rho_0Q}{2\pi r}e^{j(wt-kr)}$,任意方向的声压幅值相同,说明辐射是均匀的,指向性为一个圆。
声强为$I=\frac{1}{8}\rho_0c_0u_a^2(ka)^2\frac{a^2}{r^2}$
指向性的代码如下所示1。
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import j1 # 导入一阶贝塞尔函数
def calculate_D(ka_product, start=-np.pi/2, stop=np.pi/2, num=1000):
"""计算指向性函数
参数:
ka_product: k和a的乘积
start: 起始角度(默认0.0001避免除零)
stop: 终止角度(默认π)
num: 采样点数
返回:
theta数组和D数组
"""
theta = np.linspace(start, stop, num) # 生成角度数组
numerator = (2 * j1(ka_product * np.sin(theta))) # 分子保持不变
denominator = ka_product * np.sin(theta)
return theta, (numerator / denominator) # 返回计算结果
# 绘图
fig = plt.figure()
ax = fig.add_subplot(111, projection='polar') # 创建极坐标轴
theta, D = calculate_D(ka_product=3)
D = np.abs(D)
ax.plot(theta, D) # 在极坐标中绘制
ax.set_xlabel(r'$\theta$') # 角度轴标签
ax.set_title(r'ka=1',loc='left') # 更新标题
ax.grid(True)
plt.show()
# 绘图
fig, axes = plt.subplots(2, 2, figsize=(12, 12), # 新增figsize参数调整整体尺寸
subplot_kw={'projection': 'polar'})
ka_values = [1, 3, 4, 10]
for ax, ka in zip(axes.ravel(), ka_values):
theta, D = calculate_D(ka_product=ka)
D = np.abs(D)
ax.plot(theta, D)
ax.set_title(f'ka={ka}', pad=15,loc='left') # 新增loc参数设置标题位置
ax.grid(True)
plt.tight_layout()
plt.show()
# 新增笛卡尔坐标系绘图
plt.figure(figsize=(8, 6)) # 新建画布
for ka in ka_values:
theta, D = calculate_D(ka_product=10,start=0.0001,stop=np.pi*2,num=1000)
x = np.abs(ka * np.sin(theta))
plt.plot(x, D, label=f'ka={ka}')
# 新增过零点检测
zero_crossings = np.where(np.diff(np.sign(D)))[0] # 检测符号变化点
if len(zero_crossings) > 0:
x_zeros = x[zero_crossings] + np.diff(x)[zero_crossings] * (-D[zero_crossings]/(D[zero_crossings+1] - D[zero_crossings]))
plt.scatter(x_zeros, np.zeros_like(x_zeros), color='red', marker='x', s=50, zorder=5, label='Zero Crossing')
# 新增数值标注
for xz in x_zeros:
plt.text(xz, -0.05, f'{xz:.2f}', # 向下偏移0.05避免重叠
ha='center', va='top',
rotation=45, fontsize=8,
color='red')
# 添加图例去重处理
handles, labels = plt.gca().get_legend_handles_labels()
by_label = dict(zip(labels, handles))
plt.xlabel(r'kasin($\theta$)')
plt.ylabel(r'$\frac{2J_1(kasin(\theta))}{kasin(\theta)}$', rotation=0)
plt.legend(by_label.values(), by_label.keys())
plt.grid(True)
plt.tight_layout()
plt.show()
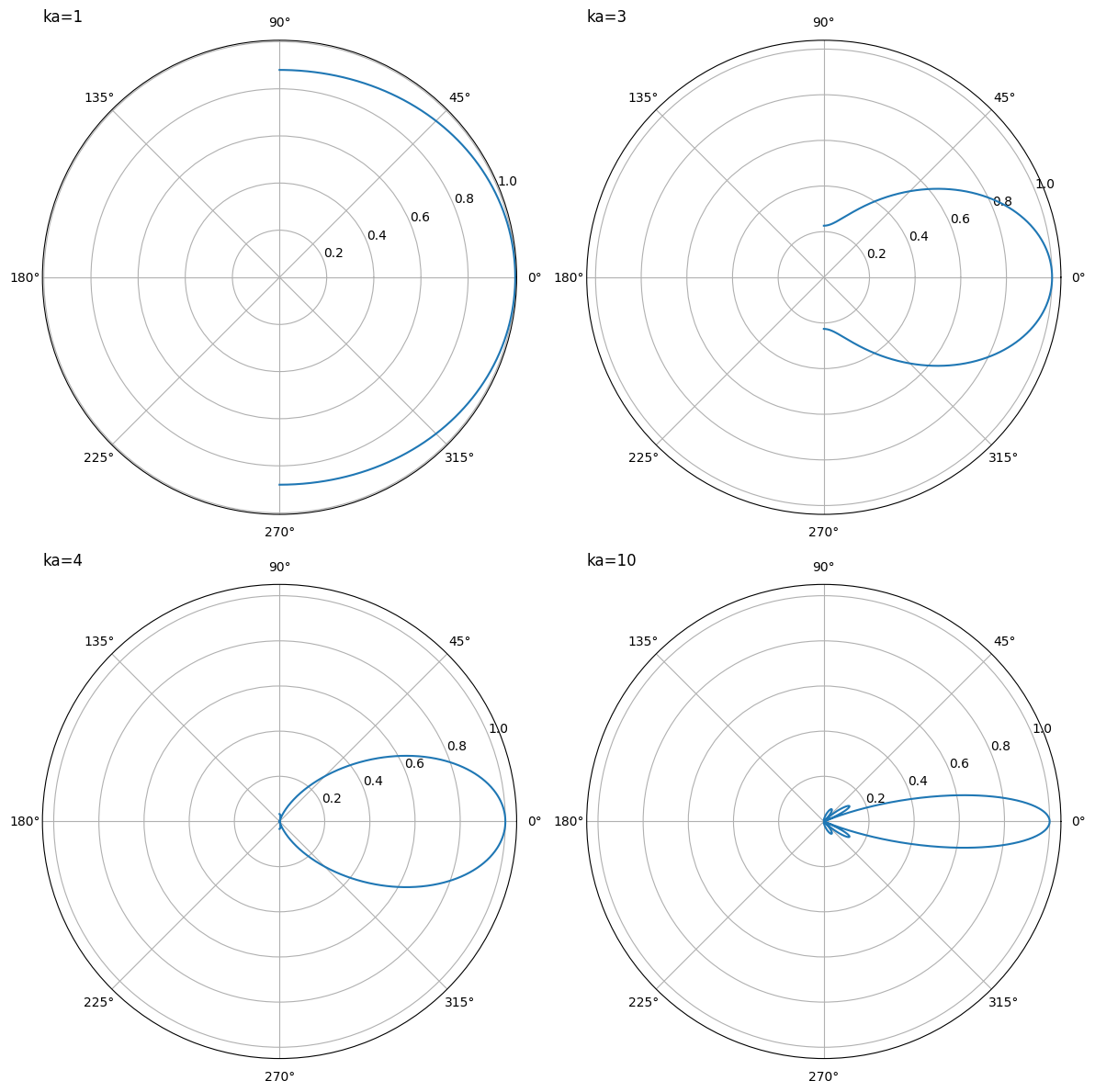
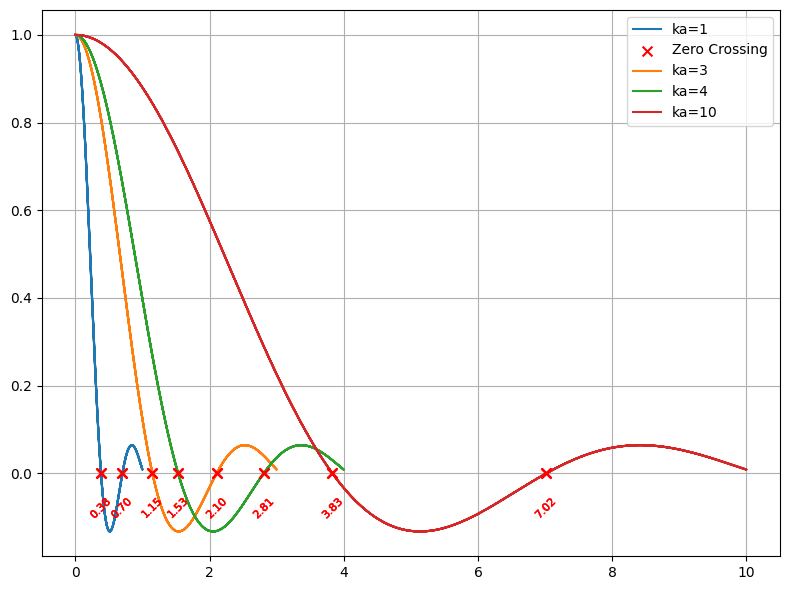
ka=10,表示:$ka=\frac{2\pi}{\lambda}a=10$,即$a=1.6\lambda$。半径越大,主极的夹角越小,指向性越强。
近场
近场研究的是中心轴上的声场,即x轴。观察点P在x轴上,不再是xoz平面上。则θ=0。
远场针对h做了近似。
$|h|=\sqrt{r^2+\sigma^2-2\overrightarrow{r} \times \overrightarrow{\sigma }}=\sqrt{r^2+\sigma^2-2|r||\sigma| (sin\theta cos\varphi )}=r\sqrt{1+\frac{\sigma^2}{r^2}-\frac{2 \sigma}{r}sin\theta cos\varphi}$
由于r>>a(或者σ),故$\frac{\sigma^2}{r^2} \approx 0$,所以:
$|h|=r\sqrt{1-\frac{2 \sigma}{r}sin\theta cos\varphi}$
近场时,r不是远大于a,使用z表示r。由于θ=0,上式变为:
$|h|=\sqrt{z^2+\sigma^2-2\overrightarrow{z} \times \overrightarrow{\sigma }}=\sqrt{z^2+\sigma^2-2|z||\sigma| (sin\theta cos\varphi )}=\sqrt{z^2+\sigma^2}$
对于活塞上所取的环元$\sigma$到$\sigma+d\sigma$,由于$d\sigma<<\sigma$,故可以认为环元上所有点到观测点P的距离基本一样,即|h|一样。
对dp进行积分可得p点的声压为:
$p=j\frac{\rho_0C_0k}{2\pi h}\int dQ_0e^{j(wt-kh)}=j\frac{\rho_0C_0k}{2\pi h} \int u_a dS e^{j(wt-kh)}=j\frac{\rho_0C_0k}{2\pi h} u_a e^{j(wt-kh)} \int dS $
环元面积为:$dS=d\sigma \int dl=d\sigma \int\sigma d\varphi=\sigma d\sigma \int d\varphi=\sigma d\sigma 2\pi=2\pi\sigma d\sigma$
$p=j\frac{\rho_0C_0k}{2\pi h} u_a e^{j(wt-kh)}\int_0^{a} 2\pi\sigma d\sigma$
由于$h^2=z^2+\sigma^2$,则$\frac{\partial h^2}{\partial \sigma}=2\sigma$
$\frac{\partial h^2}{\partial h}\frac{\partial h}{\partial \sigma}=2\sigma$
$2h\partial h=2\sigma\partial \sigma$
推导出:$dS=2\pi\sigma d\sigma=2\pi h\partial h$
σ=0时,h=z;σ=a时,h=R=$\sqrt{z^2+a^2}$
故p为:
$p=j\frac{\rho_0C_0k}{2\pi h} u_a e^{j(wt-kh)}\int_0^{a} 2\pi\sigma d\sigma=j\rho_0C_0ku_ae^{jwt}\int_z^Re^{-jkh}dh$
$p=j\rho_0C_0ku_ae^{jwt}[\frac{1}{-jk}e^{-jkh}|_z^R]=-\rho_0C_0u_ae^{jwt}[e^{-jkR}-e^{-jkz}]=-\rho_0C_0u_ae^{jwt}e^{-jk\frac{z+R}{z}}[e^{jk\frac{z-R}{2}}-e^{-jk\frac{z-R}{2}}]$
根据sin的欧拉公式:$sin\theta=\frac{e^{j\theta}-e^{-j\theta}}{2j}=-j\frac{e^{j\theta}-e^{-j\theta}}{2}=-e^{j\frac{\pi}{2}}\frac{e^{j\theta}-e^{-j\theta}}{2}$,最终推导p为:
$p=2\rho_0C_0u_a sin(k\frac{R-z}{2})e^{j(wt-k\frac{R+z}{2}+\frac{\pi}{2})}$
当z很小时,在$k\frac{R-z}{2}=n\pi$时,p=0;在$k\frac{R-z}{2}=n\pi+\frac{\pi}{2}$时,p最大。
$R-z=\sqrt{z^2+a^2}-z=z[\sqrt{1+\frac{a^2}{z^2}}-1]$
当z>2a时,通过特勒展开,得到$\sqrt{1+(\frac{a}{z})^2}=1+\frac{1}{2}(\frac{a}{z})^2$,上式变为:
$R-z=z[\sqrt{1+\frac{a^2}{z^2}}-1]=z[\frac{1}{2}(\frac{a}{z})^2]=\frac{a^2}{2z}$
则$sin(k\frac{R-z}{2})=sin(\frac{2\pi}{\lambda}\frac{a^2}{4z})=sin(\frac{\pi}{2}\frac{a^2}{\lambda z})$
设定$z_g=\frac{a^2}{\lambda}$,上式为:$sin(\frac{\pi}{2}\frac{z_g}{z})$
在z=zg位置,幅值最大;z>zg后不再有极大值。
z>2a时的轴声压为:
$p=2\rho_0C_0u_a sin(\frac{\pi}{2}\frac{a^2}{\lambda z})e^{j(wt-k\frac{R+z}{2}+\frac{\pi}{2})}=2\rho_0C_0u_a sin(\frac{\pi}{2}\frac{z_g}{ z})e^{j(wt-k\frac{R+z}{2}+\frac{\pi}{2})}$
$z_g=\frac{a^2}{\lambda}$为从近场过渡到远场的临界点,其值为临界距离。其中a为活塞半径,也称为孔径。如果是环状的则是内外半径的平方差。
可见活塞半径越大,临界距离越大。